科目：gzsx 来源： 题型：
| 2 |
| 2 |
| 2 |
| 2 |
科目：gzsx 来源：河南省长葛市第三实验高中2011届高三上学期第一次考试理科数学试题 题型：044
已知二次函数y＝g(x)的导函数的图像与直线y＝2x平行，且y＝g(x)在x＝－1处取得最小值m－1(m≠0)．设函数f(x)＝
(1)若曲线y＝f(x)上的点P到点Q(0，2)的距离的最小值为
，求m的值；
(2)k(k∈R)如何取值时，函数y＝f(x)－kx存在零点，并求出零点．
科目：gzsx 来源：2009年高考数学理科(广东B卷) 题型：044
已知二次函数
y＝g(x)的导函数的图像与直线y＝2x平行，且y＝g(x)在x＝－1处取得极小值m－1(m≠0)．设
．
(1)若曲线y＝f(x)上的点P到点Q(0，2)的距离的最小值为
，求m的值；
(2)k(k∈R)如何取值时，函数y＝f(x)＝kx存在零点，并求出零点．
科目：gzsx 来源：2009年高考数学文科(广东A卷) 题型：044
已知二次函数
y＝g(x)的导函数的图像与直线y＝2x平行，且y＝g(x)在x＝－1处取得极小值m－1(m≠0)．设函数
(1)若曲线y＝f(x)上的点p到点Q(0，2)的距离的最小值为
，求m的值；
(2)k(k∈R)如何取值时，函数y＝f(x)－kx存在零点，并求出零点．
科目：gzsx 来源：广西南宁二中2012届高三8月月考数学文科试题 题型：044
已知曲线C上任意一点M到点F(0，1)的距离比它到直线l：y＝－2的距离小1．
(Ⅰ)求曲线C的方程；
(Ⅱ)过点P(2，2)的直线m与曲线C交于A，B两点，设
，当△AOB的面积为
时(O为坐标原点)，求λ的值．
科目：gzsx 来源：辽宁省大连市二十四中2012届高三模拟考试数学理科试题 题型：044
已知曲线C上任意一点M到点F(0，1)的距离比它到直线l：y＝－2的距离小1．
(1)求曲线C的方程：
(2)若过点P(2，2)的直线m与曲线C交于A，B两点，设
(i)当λ＝1时，求直线m的方程：
(ii)当△AOB的面积为
时(O为坐标原点)，求λ的值．
科目：gzsx 来源：广西南宁二中2012届高三8月月考数学理科试题 题型：044
已知曲线C上任意一点M到点F(0，1)的距离比它到直线l：y＝－2的距离小1．
(Ⅰ)求曲线C的方程；
(Ⅱ)过点P(2，2)的直线m与曲线C交于A，B两点，设
，当△AOB的面积为
时(O为坐标原点)，求λ的值．
科目：gzsx 来源：陕西省西安铁一中2011届高三第二次模拟考试数学文科试题 题型：044
已知二次函数y＝g(x)的导函数的图像与直线y＝2x平行，且y＝g(x)在x＝－1处取得极小值m－1(m≠0)．设函数
．
(1)若曲线y＝f(x)上的点P到点Q(0，2)的距离的最小值为
，求m的值；
(2)k(k∈R)如何取值时，函数y＝f(x)－kx存在零点．
科目：gzsx 来源：重庆南开中学高2007级4月数学理科模拟试题 题型：044
已知曲线C上任意一点M到点F(0，1)的距离比它到直线l：y＝－2的距离小1．
(1)求曲线C的方程；
(2)若过点P(2，2)的直线m与曲线C交于A，B两点，设
(λ＞1)，且ΔAOB的面积为
，(O为坐标原点)，求实数λ的值．
科目：gzsx 来源：101网校同步练习 高二数学 苏教版(新课标·2004年初审) 苏教版 题型：022
动点P到点A(0，2)的距离和到直线l：y＝－2的距离相等，则动点P的轨迹方程为________
科目：gzsx 来源：江西省临川十中2011－2012学年高二下学期期中考试数学文科试题 题型：022
点P是抛物线
y2＝x上一个动点，则点P到点A(0，1)的距离与点P到直线x＝－1的距离和的最小值是________．
科目：gzsx 来源：江苏省前黄高级中学2007届高三数学周练试卷[原创]旧人教 题型：044
已知动点M到A(0，2)的距离减去它到x轴的距离的差是2；求动点M的轨迹方程C；讨论当A和B满足什么关系时，直线A(x－4)＋B(y－2)＝0
且不全为零)与曲线C有两个交点．
科目：gzsx 来源： 题型：
科目：gzsx 来源：2004全国各省市高考模拟试题汇编(天利38套)·数学 题型：044
已知定点A(－1，0)、B(1，0)，动点M满足：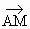
·
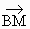等于点M到点C(0，1)距离平方的k倍．
(Ⅰ)试求动点M的轨迹方程，并说明方程所表示的曲线；
(Ⅱ)(文)当k＝2时，求|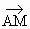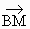＋|最大值和最小值．
(理)当k＝2时，求|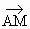＋2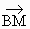|最大值和最小值．
科目：gzsx 来源：浙江省温州十校联合体2010届高三上学期期中考试数学文科试题 题型：044
已知曲线C上的动点P(x，y)满足到点F(0，1)的距离比到直线y＝－2的距离小1．
(Ⅰ)求曲线C的方程；
(Ⅱ)过点F的直线l与曲线C交于A、B两点．
(ⅰ)过A、B两点分别作抛物线的切线，设其交点为M，证明：MA⊥MB；
(ⅱ)是否在y轴上存在定点Q，使得无论AB怎样运动，都有∠AQF＝∠BQF？证明你的结论．
上的一个动点，则点P到点（0,2）的距离与P到该抛物线准线的距离之和的最小值为
B．３ C．
D．