科目：gzsx 来源： 题型：
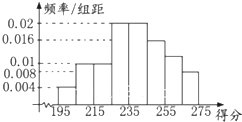（2013•郑州一模）某高校组织自主招生考试，共有2000名优秀学生参加笔试，成绩均介于195分到275分之间，从中随机抽取50名同学的成绩进行统计，将统计结果按如下方式分成八组：第一组[195，205），第二组[205，215），…，第八组[265，275]．如图是按上述分组方法得到的频率分布直方图，且笔试成绩在260分（含260分）以上的同学进入面试．| 1 | 2 |
科目：gzsx 来源： 题型：
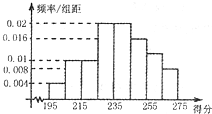（2013•郑州一模）某高校组织自主招生考试，共有2000名优秀学生参加笔试，成绩均介于195分到275分之间，从中随机抽取50名同学的成绩进行统计，将统计结果按如下方式分成八组：第一组[195，205），第二组[205，215），…，第八组[265，275]．如图是按上述分组方法得到的频率分 布直方图，且笔试成绩在260分（含260分）以上的同学进入面试．| 1 | 2 |
科目：gzsx 来源： 题型：
某市有210名初中学生参加数学竞赛预赛，随机调阅了60名学生的答卷，成绩列表如下：
| 成绩（分） | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数分布 | 0 | 0 | 0 | 6 | 15 | 21 | 12 | 3 | 3 | 0 |
（1）求样本的数学平均成绩及标准差；（精确到0.01）
（2）若总体服从正态分布，求此正态曲线的近似方程.
科目：gzsx 来源： 题型：
).某市有280名高一学生参加计算机操作比赛，等级分为10分，随机调阅了60名学生的成绩，见下表：
成绩（分） | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
人数（个） | 0 | 0 | 0 | 6 | 15 | 21 | 12 | 3 | 3 | 0 |
（1）求样本的平均成绩和标准差；
（2）若总体服从正态分布，求正态曲线的近似方程（提示：μ,σ分别可用样本的均值和标准差估计）；
（3）若规定比赛成绩在7分或7分以上的学生参加省级比赛，试估计有多少学生可以进入省级比赛?（参考数值:φ(0.82)=0.793 9）
科目：gzsx 来源：设计选修数学－2-3人教A版 人教A版 题型：044
在标准正态分布中我们常设P(X＜x0)＝Φ(x0)，根据标准正态曲线的对称性有性质：P(X＞x0)＝1－Φ(x0)．若X－N(μ，σ2)，记P(X＜x0)＝F(x0)＝Φ(
)．
某市有280名高一学生参加计算机操作比赛，等级分为10分，随机调阅了60名学生的成绩，见下表：
(1)求样本的平均成绩和标准差；
(2)若总体服从正态分布，求正态曲线的近似方程(提示：μ，σ分别可用样本的均值和标准差估计)；
(3)若规定比赛成绩在7分或7分以上的学生参加省级比赛，试估计有多少学生可以进入省级比赛？(参考数值：φ(0.82)＝0.793 9)
科目：gzsx 来源： 题型：
成绩（分） | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
人数分布 | 0 | 0 | 0 | 6 | 15 | 21 | 12 | 3 | 3 | 0 |
（1）求样本的数学平均成绩及标准差（精确到0.01）；
（2）若总体服从正态分布，求此正态曲线的近似方程.
科目：gzsx 来源： 题型：
某高校组织自主招生考试，共有2000名优秀学生参加笔试，成绩介于195分到275分之间，从中随机抽取50名学生的成绩进行统计，将统计结果按如下方式分成8组：第一组
，第二组
，…，第八组
．如图是按上述分组方法得到的频率分布直方图，且笔试成绩在260分（含260分）以上的同学进入面试．
（1） 估计所有参加笔试的2000名学生中，参加面试的学生人数；
（2） 面试时，每位考生抽取二个问题，若两个问题全答错，则不能取得该校的自主招生的资格；若二个问题均回答正确且笔试成绩在270分以上，则获得A类资格；其它情况下获B类资格．现已知某中学有两人获得面试资格，且仅有一人笔试成绩为270分以上，在回答两个面试问题时，两人对每一个问题正确回答的概率均为
，求恰有一位同学获得该高校B类资格的概率．
科目：gzsx 来源：2013年河南省郑州市高考数学一模试卷（理科）（解析版） 题型：解答题
，用随机变量X表示该中学获得B类资格的人数，求X的分布列及期望EX．
科目：gzsx 来源： 题型：
科目：gzsx 来源： 题型：
（2009•宁波模拟）某市十所重点中学进行高三联考，共有5000名考生，为了了解数学学科的学习情况，现从中随机抽出若干名学生在这次测试中的数学成绩，制成如图所示的频率分布直方图．据此估计全体考生中120分及以上的学生数为科目：gzsx 来源： 题型：
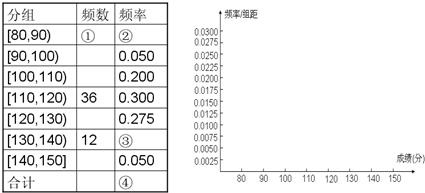
某市十所重点中学进行高三联考，共有5000名考生，为了了解数学学科的学习情况，现从中随机抽出若干名学生在这次测试中的数学成绩，制成如下频率分布表：| 分组 | 频数 | 频率 |
| [80，90） | ① | ② |
| [90，100） | 0.050 | |
| [100，110） | 0.200 | |
| [110，120） | 36 | 0.300 |
| [120，130） | 0.275 | |
| [130，140） | 12 | ③ |
| [140，150） | 0.050 | |
| 合计 | ④ |
科目：gzsx 来源： 题型：
某市十所重点中学进行高三联考，共有5000名考生，为了了解数学学科的学习情况，现从中随机抽出若干名学生在这次测试中的数学成绩，制成如下频率分布表：| 分组 | 频数 | 频率 |
| [80，90） | ① | ② |
| [90，100） | 0.050 | |
| [100，110） | 0.200 | |
| [110，120） | 36 | 0.300 |
| [120，130） | 0.275 | |
| [130，140） | 12 | ③ |
| [140，150] | 0.050 | |
| 合计 | ④ |
科目：gzsx 来源： 题型：
（12分）某市十所重点中学进行高三联考，共有5000名考生，为了了解数学学科的学习情况，现从中随机抽出若干名学生在这次测试中的数学成绩，制成如下频率分布表：
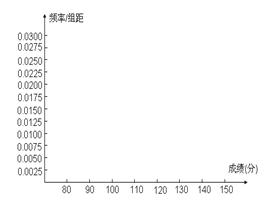
（1）根据上面频率分布表，求①，②，③，④处的数值
（2）在所给的坐标系中画出区间[80，150]上的频率分布直方图；
(3)从整体中任意抽取3个个体,成绩落在［105，120］中的个体数目为ξ ,求ξ的分布列和数
学期望.科目：gzsx 来源： 题型：
（本小题满分12分）某市十所重点中学进行高三联考，共有5000名考生，为了了解数学学科的学习情况，现从中随机抽出若干名学生在这次测试中的数学成绩，制成如下频率分布表：
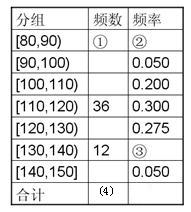
（1）根据上面频率分布表，求①，②，③，④处的数值
（2）在所给的坐标系中画出区间[80，150]上的频率分布直方图；
(3)从整体中任意抽取3个个体,成绩落在［105，120］中的个体数目为ξ ,求ξ的分布列和数学期望.
科目：gzsx 来源：吉林省2010年高三年级第八次模拟考试数学试题（理） 题型：解答题
某市十所重点中学进行高三联考，共有5000名考生，为了了解数学学科的学习情况，现从中随机抽出若干名学生在这次测试中的数学成绩，制成如下频率分布表：
（1）根据上面的频率分布表，求①，②，③，④处的数值；
（2）根据上面的频率分布表,在所给的坐标系中画出在区间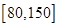
上的频率分布直方图;
（3）如果把表中的频率近似地看作每个学生在这次考试中取得相应成绩的概率，那么从总体中任意抽取3个个体,成绩落在
中的个体数为
,求的分布列和数学期望．
|
分组 |
频数 |
频率 |
|
|
① |
② |
|
|
|
0．050 |
|
|
|
0．200 |
|
|
36 |
0．300 |
|
|
|
0．275 |
|
|
12 |
③ |
|
|
|
0．050 |
|
合计 |
④ |
|
科目：gzsx 来源： 题型：
（本小题满分13分）
某市十所重点中学进行高三联考，共有5000名考生，为了了解数学学科的学习情况，
现从中随机抽出若干名学生在这次测试中的数学成绩，制成如下频率分布表：
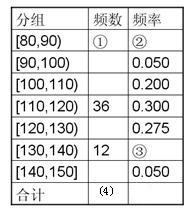
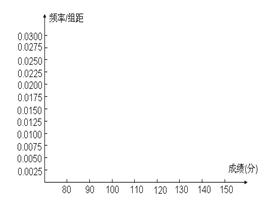
（1）根据上面频率分布表，求①，②，③，④处的数值
（2）在所给的坐标系中画出区间[80，150]上的频率分布直方图；
(3)从整体中任意抽取3个个体,成绩落在［105，120］中的个体数目为ξ ,求ξ的分布列和数
学期望.
科目：gzsx 来源：2012-2013学年湖北省襄阳市襄州、枣阳、宜城、曾都一中联考高二（上）期中数学试卷（解析版） 题型：解答题
| 分组 | 频数 | 频率 |
| [80，90） | ① | ② |
| [90，100） | 0.050 | |
| [100，110） | 0.200 | |
| [110，120） | 36 | 0.300 |
| [120，130） | 0.275 | |
| [130，140） | 12 | ③ |
| [140，150] | 0.050 | |
| 合计 | ④ |
科目：gzsx 来源： 题型：
（本小题满分8分）某市十所重点中学进行高三联考，共有5000名考生，为了了解数学学科的学习情况，现从中随机抽出若干名学生在这次测试中的数学成绩，制成如下频率分布表：
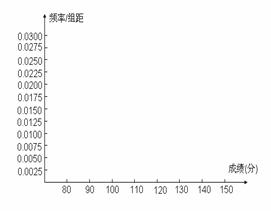
（Ⅰ）根据上面频率分布表，推出①，②，③，④处的数值分别为 ，
， ， ；
（Ⅱ）在所给的坐标系中画出区间上的频率分布直方图；
（Ⅲ）根据题中信息估计总体：（ⅰ）120分及以上的学生数；（ⅱ）平均分；（ⅲ）成绩落在［126，150］中的概率.
科目：gzsx 来源： 题型：解答题
某市十所重点中学进行高三联考，共有5000名考生，为了了解数学学科的学习情况，现从中随机抽出若干名学生在这次测试中的数学成绩，制成如下频率分布表：| 分组 | 频数 | 频率 |
| [80，90） | ① | ② |
| [90，100） | 0.050 | |
| [100，110） | 0.200 | |
| [110，120） | 36 | 0.300 |
| [120，130） | 0.275 | |
| [130，140） | 12 | ③ |
| [140，150） | 0.050 | |
| 合计 | ④ |
科目：gzsx 来源：2012-2013学年山西大学附中高三（上）第二次月考数学试卷（文科）（解析版） 题型：解答题
