如图在平面直角坐标系中,点A、B在X轴上,且OB=OC=3,OA=OD=1答案解析
科目:czsx
来源:
题型:
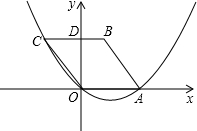
如图,平面直角坐标系中,点C(-3,4),A为x轴正半轴上一点,已知四边形OABC为菱形,BC交y轴于点D
(1)求过点A、O、C的抛物线解析式;
(2)线段CB上是否存在这样的点P:当点P绕点O顺时针旋转90°后恰好落在(1)所求的抛物线上?若存在,求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
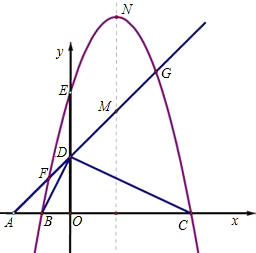
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)判断△BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
(2013•秀洲区二模)如图①,平面直角坐标系中,直线
y=x+3分别交x轴、y轴于点A、B,OC⊥AB于点C,D是AB的中点.动点P从A出发沿折线AD→DO方向以每秒1个单位长度的速度向终点O运动,同时动点Q从点D出发沿折线DO→OB方向以相同的速度运动.设点P的运动时间为t秒,当点P到达O点时P、Q同时停止运动.
(1)求OD的长;
(2)当点P在AD上运动时,设△DPQ的面积为S,求S关于t的函数关系式,并求出S的最大值;
(3)如图②,当点P在DO上、点Q在OB上运动时,PQ与OC交于点E,当t为何值时,△OPE为等腰三角形?

查看答案和解析>>
科目:czsx
来源:
题型:
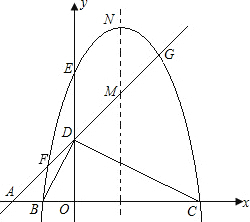
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,DB⊥DC,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M.点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)是否存在点P,使得以P、Q、M为顶点的三角形与△AOD相似?若存在,求出满足条件的点P的坐标;若不存在,请说明理由;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
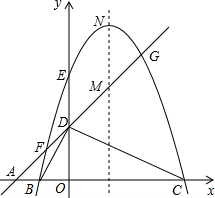
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y 轴上,OA=OD=2,OC=OE=4,2OB=OD,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M.点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)是否存在点P,使得以P、Q、M为顶点的三角形与△AOD相似?若存在,求出满足条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,平面直角坐标系中,点B的坐标为(1,2),过点B作x轴的垂线,垂足为A,连
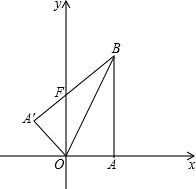
接OB,将△OAB沿OB折叠,使点A落在点A′处,A′B与y轴交于点F.
(1)求证:OF=BF;
(2)求BF的长;
(3)求过点A′的双曲线的解析式.
查看答案和解析>>
科目:czsx
来源:
题型:
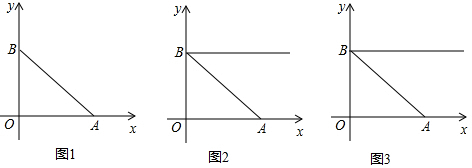
如图,平面直角坐标系中,点A(4,0),直线AB与y轴交于点B,S
△AOB=6,点P从点A出发,以每秒1个单位的速度沿x轴正方向运动.
(1)求B点坐标.
(2)过点B作射线L∥x轴,动点Q从B出发,以每秒2个单位的速度,沿射线L运动.若动点P、Q同时运动,过点A作AC⊥AB,射线AC与射线PQ、射线L分别交于点C、K.设运动时间为t秒,线段KQ的长为y个单位.求y与t的函数关系式,并直接写出自变量t的取值范围.
(3)在(2)的条件下,若D为BC中点.在点P、Q运动过程中是否存在t值,以A、C、D、Q为顶点的四边形是平行四边形?若存在,求出t值;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

(2013•东阳市模拟)如图,平面直角坐标系中,点A(0,4),B(3,0),D、E在x轴上,F为平面上一点,且EF⊥x轴,直线DF与直线AB互相垂直,垂足为H,△AOB≌△DEF,设BD=h.
(1)若F坐标(7,3),则h=
0
0
,若F坐标(-10,-3),则DH=
;
(2)如h=
,则相对应的F点存在
4
4
个,并请求出恰好在抛物线y=
-x2+x+4上的点F的坐标;
(3)请求出4个值,满足以A、H、F、E为顶点的四边形是梯形.
查看答案和解析>>
科目:czsx
来源:
题型:
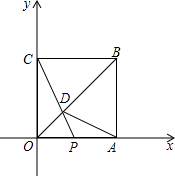
将边长为4的正方形在如图的平面直角坐标系中.点P是OA上的一个动点,且从点O向点A运动.连接CP交对角线OB于点D,连接AD.
(1)求证:△OCD≌△OAD;
(2)若△OCD的面积是四边形OABC面积的
,求P点的坐标;
(3)若点P从点O运动到点A后,再继续从点A运动到点B,在整个运动过程中,当△OCD恰为等腰三角形时,请直接写出点P的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
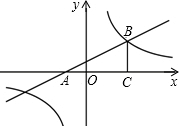
如图,平面直角坐标系中,直线
y=x+与x轴交于点A,与双曲线
y=在第一象限内交于点B,BC丄x轴于点C,OC=2AO.求双曲线的解析式.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,平面直角坐标系中,点A、B分别在x、y轴上,点B的坐标为(0,1),∠BAO=30°.
(1)求AB的长度;
(2)以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点D.求证:BD=OE;
(3)在(2)的条件下,连接DE交AB于F.求证:F为DE的中点.
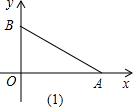
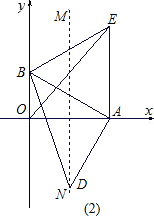
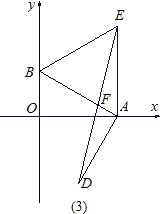
查看答案和解析>>
科目:czsx
来源:
题型:
如图①,平面直角坐标系中,点A、B在x轴上,点C在第一象限,AC=BC,点D、E分别是AC、BC的中点.已知A、D两点的坐标分别为(-3,0)、(0,4),
(1)直接写出下列各点的坐标:
B
(9,0)
(9,0)
;C
(3,8)
(3,8)
;E
(6,4)
(6,4)
;
(2)如图②动点P从点A出发,沿A→D→E的方向向点E运动(不与E重合),同时动点M从点D出发,沿D→E→B的方向向点B运动(不与B重合),P、M运动的速度均为每秒1个单位,过点P的直线l与线段BC平行,交线段AB于点Q,设运动时间为t秒(t>0),
①直接写出t的取值:
当
5≤t<11
5≤t<11
时,四边形PQBE为平行四边形;
当
t=6
t=6
时,四边形PQBM为菱形;
②求△BQM的面积S与运动时间t的函数关系式,并写出相应的t的取值范围.
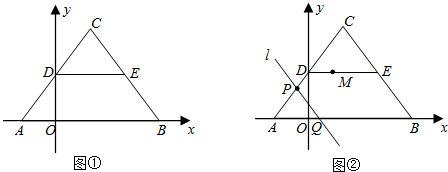
查看答案和解析>>
科目:czsx
来源:
题型:
如图,平面直角坐标系中,点O(0,0)、A(1,0),过点A作x轴的垂线交直线y=x于点B

,以O为圆心,OA为半径的圆交y轴于C、D两点,抛物线y=x
2+bx+c经过B、D.
(1)求b,c的值;
(2)设抛物线的对称轴交x轴于点E,连接DE并延长交⊙O于F,求EF的长;
(3)若⊙O交x轴负半轴于点G,过点C作⊙O的切线交DG的延长线于点P.
探究:点P是否在抛物线上?请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

已知:如图,平面直角坐标系中,点A、B的坐标分别是A(1,4);B(3,0),以AB为直径的圆M与y轴相交于点C、D(点C在D的下方).
(1)求直线AB的函数解析式和线段AB的长;
(2)判断△ABC的形状,并说明理由;
(3)若点P在以AB为直径的圆M上,且∠BAP=∠OBC,设直线AP与x轴的交点为Q,求点Q的坐标.
查看答案和解析>>
科目:czsx
来源:2010年湖北省天门市中考数学试卷(解析版)
题型:解答题
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,DB⊥DC,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M.点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)是否存在点P,使得以P、Q、M为顶点的三角形与△AOD相似?若存在,求出满足条件的点P的坐标;若不存在,请说明理由;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.

查看答案和解析>>
科目:czsx
来源:2013年四川省成都市中考数学模拟试卷(十六)(解析版)
题型:解答题
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)判断△BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.(湖北潜江中考25题改编)

查看答案和解析>>
科目:czsx
来源:2012年四川省成都市金牛区中考数学二模试卷(解析版)
题型:解答题
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)判断△BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.(湖北潜江中考25题改编)

查看答案和解析>>
科目:czsx
来源:2011年浙江省杭州市中考数学模拟试卷(12)(解析版)
题型:解答题
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,DB⊥DC,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M.点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)是否存在点P,使得以P、Q、M为顶点的三角形与△AOD相似?若存在,求出满足条件的点P的坐标;若不存在,请说明理由;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
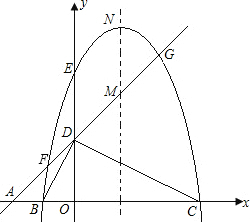 如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,DB⊥DC,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M.点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,DB⊥DC,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M.点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)是否存在点P,使得以P、Q、M为顶点的三角形与△AOD相似?若存在,求出满足条件的点P的坐标;若不存在,请说明理由;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:czsx
来源:2010年湖北省潜江市中考数学试卷(解析版)
题型:解答题
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,DB⊥DC,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M.点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)是否存在点P,使得以P、Q、M为顶点的三角形与△AOD相似?若存在,求出满足条件的点P的坐标;若不存在,请说明理由;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.

查看答案和解析>>

 如图,平面直角坐标系中,点C(-3,4),A为x轴正半轴上一点,已知四边形OABC为菱形,BC交y轴于点D
如图,平面直角坐标系中,点C(-3,4),A为x轴正半轴上一点,已知四边形OABC为菱形,BC交y轴于点D  如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
 如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,DB⊥DC,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M.点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,DB⊥DC,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M.点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q. 如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y 轴上,OA=OD=2,OC=OE=4,2OB=OD,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M.点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y 轴上,OA=OD=2,OC=OE=4,2OB=OD,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M.点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q. 接OB,将△OAB沿OB折叠,使点A落在点A′处,A′B与y轴交于点F.
接OB,将△OAB沿OB折叠,使点A落在点A′处,A′B与y轴交于点F.
 (2013•东阳市模拟)如图,平面直角坐标系中,点A(0,4),B(3,0),D、E在x轴上,F为平面上一点,且EF⊥x轴,直线DF与直线AB互相垂直,垂足为H,△AOB≌△DEF,设BD=h.
(2013•东阳市模拟)如图,平面直角坐标系中,点A(0,4),B(3,0),D、E在x轴上,F为平面上一点,且EF⊥x轴,直线DF与直线AB互相垂直,垂足为H,△AOB≌△DEF,设BD=h. 将边长为4的正方形在如图的平面直角坐标系中.点P是OA上的一个动点,且从点O向点A运动.连接CP交对角线OB于点D,连接AD.
将边长为4的正方形在如图的平面直角坐标系中.点P是OA上的一个动点,且从点O向点A运动.连接CP交对角线OB于点D,连接AD. 如图,平面直角坐标系中,直线y=
如图,平面直角坐标系中,直线y=


 ,以O为圆心,OA为半径的圆交y轴于C、D两点,抛物线y=x2+bx+c经过B、D.
,以O为圆心,OA为半径的圆交y轴于C、D两点,抛物线y=x2+bx+c经过B、D. 已知:如图,平面直角坐标系中,点A、B的坐标分别是A(1,4);B(3,0),以AB为直径的圆M与y轴相交于点C、D(点C在D的下方).
已知:如图,平面直角坐标系中,点A、B的坐标分别是A(1,4);B(3,0),以AB为直径的圆M与y轴相交于点C、D(点C在D的下方).



 如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,DB⊥DC,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M.点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,DB⊥DC,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M.点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.