精英家教网 >
试题搜索列表 >（3）根据（1）（2）的规律，试判断能否在1，2，3，…，2012，2013，共2013个数字的每两个数字之间添上“+”或“-”，使它们的和为0？若能，请说明添法；若不能，请说明理由．
（3）根据（1）（2）的规律，试判断能否在1，2，3，…，2012，2013，共2013个数字的每两个数字之间添上“+”或“-”，使它们的和为0？若能，请说明添法；若不能，请说明理由．答案解析
科目：czsx
来源：
题型：
（1）有1，2，3，…，11，12共12个数字，请在每两个数字之间添上“+”或“-”，使它们的和为0；
（2）若有1，2，3，…，2007，2008共2008个数字，请在每两个数字之间添上“+”或“-”，使它们的和为0；
（3）根据（1）（2）的规律，试判断能否在1，2，3，…，2012，2013，共2013个数字的每两个数字之间添上“+”或“-”，使它们的和为0？若能，请说明添法；若不能，请说明理由．
查看答案和解析>>
科目：czsx
来源：不详
题型：解答题
（1）有1，2，3，…，11，12共12个数字，请在每两个数字之间添上“+”或“-”，使它们的和为0；
（2）若有1，2，3，…，2007，2008共2008个数字，请在每两个数字之间添上“+”或“-”，使它们的和为0；
（3）根据（1）（2）的规律，试判断能否在1，2，3，…，2012，2013，共2013个数字的每两个数字之间添上“+”或“-”，使它们的和为0？若能，请说明添法；若不能，请说明理由．
查看答案和解析>>
科目：czsx
来源：
题型：解答题
（1）有1，2，3，…，11，12共12个数字，请在每两个数字之间添上“+”或“-”，使它们的和为0；
（2）若有1，2，3，…，2007，2008共2008个数字，请在每两个数字之间添上“+”或“-”，使它们的和为0；
（3）根据（1）（2）的规律，试判断能否在1，2，3，…，2012，2013，共2013个数字的每两个数字之间添上“+”或“-”，使它们的和为0？若能，请说明添法；若不能，请说明理由．
查看答案和解析>>
科目：czsx
来源：同步训练与评价·数学·七年级·上
题型：044
观察下列各式：
(1)21＝2，22＝4，23＝8，24＝16，25＝32
(2)43＝(22)3＝26，83＝(23)3＝29
根据上述两组算式所揭示的规律．试判断82003的个位数字是多少？
查看答案和解析>>
科目：czsx
来源：
题型：
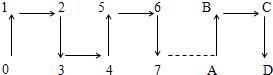
12、根据下图中箭头所指的规律，试判断数字2008应该在（ ）位置．
查看答案和解析>>
科目：czsx
来源：
题型：
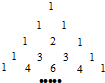
15、如图是非常著名的“杨辉三角形”，根据图中数据的规律，试判断第6行的数据之和为
32
．
查看答案和解析>>
科目：czsx
来源：
题型：
如图1的平面直角坐标系中，等腰直角三角形A
0B
1A
1的斜边A
0A
1落在y轴的正半轴上，A
0A
1=2，点A
0与原点O重合．二次函数y=ax
2的图象恰好经过B
1．
（1）求二次函数的解析式；
（2）在y轴的正半轴依次取点A
2，A
3，A
4，…，A
n，使得以A
1A
2，A
2A
3，A
3A
4，…，A
n-1A
n，为斜边的等腰直角三角形△A
1B
2A
2，△A
2B
3A
3，△A
3B
4A
4，…，△A
n-1B
nA
n的顶点B
2，B
3，B
4，…，B
n分别落在二次函数y=ax
2的图象上（如图2）．完成下列填空：A
1A
2=
，A
2A
3=
；
（3）根据（2）观察分析得到的规律，试写出A
n-1A
n的长：A
n-1A
n=
（用n的代数式表示）．
查看答案和解析>>
科目：czsx
来源：
题型：阅读理解
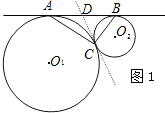
阅读下列材料：
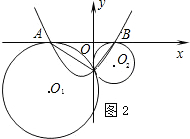
如图1，⊙O
1和⊙O
2外切于点C，AB是⊙O
1和⊙O
2外公切线，A、B为切点，
求证：AC⊥BC
证明：过点C作⊙O
1和⊙O
2的内公切线交AB于D，
∵DA、DC是⊙O
1的切线
∴DA=DC．
∴∠DAC=∠DCA．
同理∠DCB=∠DBC．
又∵∠DAC+∠DCA+∠DCB+∠DBC=180°，
∴∠DCA+∠DCB=90°．
即AC⊥BC．
根据上述材料，解答下列问题：
（1）在以上的证明过程中使用了哪些定理？请写出两个定理的名称或内容；
（2）以AB所在直线为x轴，过点C且垂直于AB的直线为y轴建立直角坐标系（如图2），已知A、B两点的坐标为（-4，0），（1，0），求经过A、B、C三点的抛物线y=ax
2+bx+c的函数解析式；
（3）根据（2）中所确定的抛物线，试判断这条抛物线的顶点是否落在两圆的连心O
1O
2上，并说明理由．
查看答案和解析>>
科目：czsx
来源：
题型：
己知两个任意正数a和b，有下列命题：
（1）若a+b=2，则
≤1（2）若a+b=
，则
≤（3）若a+b=
，则
≤；根据以上三个命题所提供的规律，试猜想出a+b与
应满足的最佳关系式：
．
查看答案和解析>>
科目：czsx
来源：2002年全国中考数学试题汇编《二次函数》（05）（解析版）
题型：解答题
（2004•呼和浩特）阅读下列材料：
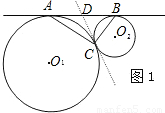
如图1，⊙O
1和⊙O
2外切于点C，AB是⊙O
1和⊙O
2外公切线，A、B为切点，
求证：AC⊥BC
证明：过点C作⊙O
1和⊙O
2的内公切线交AB于D，
∵DA、DC是⊙O
1的切线
∴DA=DC．
∴∠DAC=∠DCA．
同理∠DCB=∠DBC．
又∵∠DAC+∠DCA+∠DCB+∠DBC=180°，
∴∠DCA+∠DCB=90°．
即AC⊥BC．
根据上述材料，解答下列问题：
（1）在以上的证明过程中使用了哪些定理？请写出两个定理的名称或内容；
（2）以AB所在直线为x轴，过点C且垂直于AB的直线为y轴建立直角坐标系（如图2），已知A、B两点的坐标为（-4，0），（1，0），求经过A、B、C三点的抛物线y=ax
2+bx+c的函数解析式；
（3）根据（2）中所确定的抛物线，试判断这条抛物线的顶点是否落在两圆的连心O
1O
2上，并说明理由．
查看答案和解析>>
科目：czsx
来源：
题型：解答题
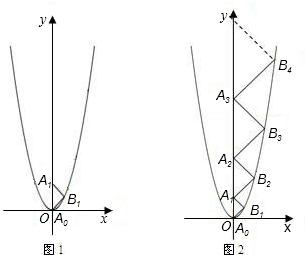
如图1的平面直角坐标系中，等腰直角三角形A0B1A1的斜边A0A1落在y轴的正半轴上，A0A1=2，点A0与原点O重合．二次函数y=ax2的图象恰好经过B1．
（1）求二次函数的解析式；
（2）在y轴的正半轴依次取点A2，A3，A4，…，An，使得以A1A2，A2A3，A3A4，…，An-1An，为斜边的等腰直角三角形△A1B2A2，△A2B3A3，△A3B4A4，…，△An-1BnAn的顶点B2，B3，B4，…，Bn分别落在二次函数y=ax2的图象上（如图2）．完成下列填空：A1A2=______，A2A3=______；
（3）根据（2）观察分析得到的规律，试写出An-1An的长：An-1An=______（用n的代数式表示）．
查看答案和解析>>
科目：czsx
来源：2009年广东省汕头市潮阳区中考数学模拟试卷（解析版）
题型：解答题
（2009•潮阳区模拟）如图1的平面直角坐标系中，等腰直角三角形A
B
1A
1的斜边A
A
1落在y轴的正半轴上，A
A
1=2，点A
与原点O重合．二次函数y=ax
2的图象恰好经过B
1．
（1）求二次函数的解析式；
（2）在y轴的正半轴依次取点A
2，A
3，A
4，…，A
n，使得以A
1A
2，A
2A
3，A
3A
4，…，A
n-1A
n，为斜边的等腰直角三角形△A
1B
2A
2，△A
2B
3A
3，△A
3B
4A
4，…，△A
n-1B
nA
n的顶点B
2，B
3，B
4，…，B
n分别落在二次函数y=ax
2的图象上（如图2）．完成下列填空：A
1A
2=______，A
2A
3=______；
（3）根据（2）观察分析得到的规律，试写出A
n-1A
n的长：A
n-1A
n=______（用n的代数式表示）．
查看答案和解析>>
科目：czsx
来源：
题型：解答题
阅读下列材料：
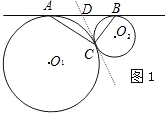
如图1，⊙O1和⊙O2外切于点C，AB是⊙O1和⊙O2外公切线，A、B为切点，
求证：AC⊥BC
证明：过点C作⊙O1和⊙O2的内公切线交AB于D，
∵DA、DC是⊙O1的切线
∴DA=DC．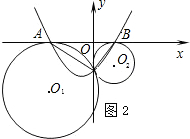
∴∠DAC=∠DCA．
同理∠DCB=∠DBC．
又∵∠DAC+∠DCA+∠DCB+∠DBC=180°，
∴∠DCA+∠DCB=90°．
即AC⊥BC．
根据上述材料，解答下列问题：
（1）在以上的证明过程中使用了哪些定理？请写出两个定理的名称或内容；
（2）以AB所在直线为x轴，过点C且垂直于AB的直线为y轴建立直角坐标系（如图2），已知A、B两点的坐标为（-4，0），（1，0），求经过A、B、C三点的抛物线y=ax2+bx+c的函数解析式；
（3）根据（2）中所确定的抛物线，试判断这条抛物线的顶点是否落在两圆的连心O1O2上，并说明理由．
查看答案和解析>>
科目：czsx
来源：2004年内蒙古呼和浩特市中考数学试卷（解析版）
题型：解答题
阅读下列材料：
如图1，⊙O
1和⊙O
2外切于点C，AB是⊙O
1和⊙O
2外公切线，A、B为切点，
求证：AC⊥BC
证明：过点C作⊙O
1和⊙O
2的内公切线交AB于D，
∵DA、DC是⊙O
1的切线
∴DA=DC．
∴∠DAC=∠DCA．
同理∠DCB=∠DBC．
又∵∠DAC+∠DCA+∠DCB+∠DBC=180°，
∴∠DCA+∠DCB=90°．
即AC⊥BC．
根据上述材料，解答下列问题：
（1）在以上的证明过程中使用了哪些定理？请写出两个定理的名称或内容；
（2）以AB所在直线为x轴，过点C且垂直于AB的直线为y轴建立直角坐标系（如图2），已知A、B两点的坐标为（-4，0），（1，0），求经过A、B、C三点的抛物线y=ax
2+bx+c的函数解析式；
（3）根据（2）中所确定的抛物线，试判断这条抛物线的顶点是否落在两圆的连心O
1O
2上，并说明理由．
查看答案和解析>>
科目：czsx
来源：2011年中考数学复习模拟试卷（15）（解析版）
题型：解答题
阅读下列材料：
如图1，⊙O
1和⊙O
2外切于点C，AB是⊙O
1和⊙O
2外公切线，A、B为切点，
求证：AC⊥BC
证明：过点C作⊙O
1和⊙O
2的内公切线交AB于D，
∵DA、DC是⊙O
1的切线
∴DA=DC．
∴∠DAC=∠DCA．
同理∠DCB=∠DBC．
又∵∠DAC+∠DCA+∠DCB+∠DBC=180°，
∴∠DCA+∠DCB=90°．
即AC⊥BC．
根据上述材料，解答下列问题：
（1）在以上的证明过程中使用了哪些定理？请写出两个定理的名称或内容；
（2）以AB所在直线为x轴，过点C且垂直于AB的直线为y轴建立直角坐标系（如图2），已知A、B两点的坐标为（-4，0），（1，0），求经过A、B、C三点的抛物线y=ax
2+bx+c的函数解析式；
（3）根据（2）中所确定的抛物线，试判断这条抛物线的顶点是否落在两圆的连心O
1O
2上，并说明理由．
查看答案和解析>>
科目：czsx
来源：2002年广西桂林市中考数学试卷（解析版）
题型：解答题
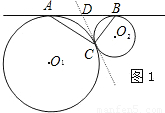
（2004•呼和浩特）阅读下列材料：
如图1，⊙O
1和⊙O
2外切于点C，AB是⊙O
1和⊙O
2外公切线，A、B为切点，
求证：AC⊥BC
证明：过点C作⊙O
1和⊙O
2的内公切线交AB于D，
∵DA、DC是⊙O
1的切线
∴DA=DC．
∴∠DAC=∠DCA．
同理∠DCB=∠DBC．
又∵∠DAC+∠DCA+∠DCB+∠DBC=180°，
∴∠DCA+∠DCB=90°．
即AC⊥BC．
根据上述材料，解答下列问题：
（1）在以上的证明过程中使用了哪些定理？请写出两个定理的名称或内容；
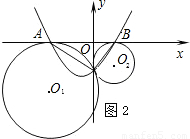
（2）以AB所在直线为x轴，过点C且垂直于AB的直线为y轴建立直角坐标系（如图2），已知A、B两点的坐标为（-4，0），（1，0），求经过A、B、C三点的抛物线y=ax
2+bx+c的函数解析式；
（3）根据（2）中所确定的抛物线，试判断这条抛物线的顶点是否落在两圆的连心O
1O
2上，并说明理由．
查看答案和解析>>
科目：czsx
来源：宣武区二模
题型：填空题
己知两个任意正数a和b，有下列命题：
（1）若a+b=2，则
≤1（2）若a+b=
，则
≤（3）若a+b=
，则
≤；根据以上三个命题所提供的规律，试猜想出a+b与
应满足的最佳关系式：______．
查看答案和解析>>
科目：czsx
来源：2007-2008学年山东省济宁市泗水县九年级（上）期中数学试卷（解析版）
题型：选择题
根据下图中箭头所指的规律，试判断数字2008应该在（ ）位置．
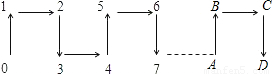
A．A
B．B
C．C
D．D
查看答案和解析>>
科目：czsx
来源：不详
题型：单选题
根据下图中箭头所指的规律，试判断数字2008应该在（ ）位置．
查看答案和解析>>
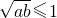
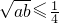
，则
，则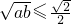
；根据以上三个命题所提供的规律，试猜想出a+b与
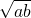应满足的最佳关系式：______．