
科目:gzsx 来源: 题型:
已知椭圆![]() +
+![]() =1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A、B两点。若AB的中点坐标为(1,-1),则E的方程为 ( )
=1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A、B两点。若AB的中点坐标为(1,-1),则E的方程为 ( )
A、![]() +
+![]() =1 B、
=1 B、![]() +
+![]() =1 C、
=1 C、![]() +
+![]() =1 D、
=1 D、![]() +
+![]() =1
=1
科目:gzsx 来源:2013年全国普通高等学校招生统一考试理科数学(新课标1卷解析版) 题型:选择题
已知椭圆 +
+ =1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A、B两点。若AB的中点坐标为(1,-1),则E的方程为 (
)
=1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A、B两点。若AB的中点坐标为(1,-1),则E的方程为 (
)
A、 +
+ =1
B、
=1
B、 +
+ =1
=1
C、 +
+ =1
D、
=1
D、 +
+ =1
=1
科目:gzsx 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练22练习卷(解析版) 题型:填空题
已知椭圆C: +
+ =1(a>0,b>0)的右焦点为F(3,0),且点(-3,
=1(a>0,b>0)的右焦点为F(3,0),且点(-3, )在椭圆C上,则椭圆C的标准方程为 .
)在椭圆C上,则椭圆C的标准方程为 .
科目:gzsx 来源: 题型:
(Ⅰ)求椭圆的方程;
(Ⅱ)在椭圆上任取三个不同点P1、P2、P3,使∠P1FP2=∠P![]() FP3=∠P3FP1,证明
FP3=∠P3FP1,证明![]() 为定值,并求此定值.
为定值,并求此定值.

题(22)图
科目:gzsx 来源:2013-2014学年湖北省武汉市高三11月调考文科数学试卷(解析版) 题型:选择题
已知椭圆E: +
+ =1(a>b>0)的右焦点为F(3,0),过点F的直线交E于A,B两点.若AB的中点坐标为(1,-1),则E的方程为( )
=1(a>b>0)的右焦点为F(3,0),过点F的直线交E于A,B两点.若AB的中点坐标为(1,-1),则E的方程为( )
A. +
+ =1
B.
=1
B. +
+ =1
C.
=1
C. +
+ =1
D.
=1
D. +
+ =1
=1
科目:gzsx 来源:浙江省绍兴市2007年高三教学质量调测数学(文) 题型:044
已知椭圆![]() 的右焦点为F(
的右焦点为F(![]() ,0)短轴长与椭圆的上顶点到右准线的距离之比为
,0)短轴长与椭圆的上顶点到右准线的距离之比为![]() .
.
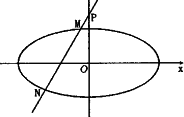
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线l:y=x+3顺次交y轴和椭圆于P、M、N三点,求![]() 的值.
的值.
科目:gzsx 来源:2013年普通高等学校招生全国统一考试全国卷理数 题型:013
已知椭圆![]() +
+![]() =1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A、B两点.若AB的中点坐标为(1,-1),则E的方程为
=1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A、B两点.若AB的中点坐标为(1,-1),则E的方程为
A.![]() +
+![]() =1
=1
B.![]() +
+![]() =1
=1
C.![]() +
+![]() =1
=1
D.![]() +
+![]() =1
=1
科目:gzsx 来源:浙江省绍兴市2007年高三教学质量调测数学(理) 题型:044
已知椭圆![]() 的右焦点为F(
的右焦点为F(![]() ,0)短轴长与椭圆的上顶点到右准线的距离之比为
,0)短轴长与椭圆的上顶点到右准线的距离之比为![]() .
.
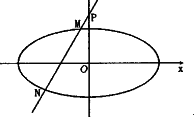
(Ⅰ)求椭圆的方程;
(Ⅱ)过点P(0,3)引直线l顺次交椭圆于M、N两点,求![]() 的取值范围.
的取值范围.
科目:gzsx 来源:2007年普通高等学校招生全国统一考试、理科数学(重庆卷) 题型:044
如图,中心在原点O的椭圆的右焦点为F(3,0),右准线l的方程为:x=12.

(1)求椭圆的方程;
(2)在椭圆上任取三个不同点P1,P2,P3,使∠P1FP2=∠P2FP3=∠P3FP1,证明
![]() 为定值,并求此定值.
为定值,并求此定值.
科目:gzsx 来源: 题型:
A.![]() =1 B.
=1 B.![]() =1
=1
C.![]() +y2=1 D.
+y2=1 D.![]() +y2=1
+y2=1
科目:gzsx 来源:2013年普通高等学校招生全国统一考试广东卷理数 题型:013
已知中心在原点的双曲线C的右焦点为F(3,0),离心率等于![]() ,在双曲线C的方程是
,在双曲线C的方程是
A.![]()
B.![]()
C.![]()
D.![]()
科目:gzsx 来源: 题型:
(08年唐山一中一模理) 已知椭圆![]() 的右焦点为F(c,0),过F作与x轴垂直的直线与椭圆相交于点P,过点P的椭圆的切线
的右焦点为F(c,0),过F作与x轴垂直的直线与椭圆相交于点P,过点P的椭圆的切线![]() 与x轴相交于点A,则点A的坐标为
与x轴相交于点A,则点A的坐标为
科目:gzsx 来源:河北省唐山一中2010高考模拟试卷(一)理 题型:填空题
已知椭圆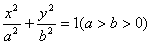 的右焦点为F(c,0),过F作与x轴垂直的直线与椭圆相交于点P,过点P的椭圆的切线
的右焦点为F(c,0),过F作与x轴垂直的直线与椭圆相交于点P,过点P的椭圆的切线 与x轴相交于点A,则点A的坐标为
___。
与x轴相交于点A,则点A的坐标为
___。
科目:gzsx 来源:2014届云南大理高二下开学考试文科数学试卷(解析版) 题型:选择题
已知双曲线 的右焦点为(3,0),则该双曲线的离心率等于 ( )
的右焦点为(3,0),则该双曲线的离心率等于 ( )
A. B.
B. C.
C. . D.
. D.
科目:gzsx 来源:2012年全国普通高等学校招生统一考试文科数学(福建卷解析版) 题型:选择题
已知双曲线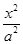 -
- =1的右焦点为(3,0),则该双曲线的离心率等于
=1的右焦点为(3,0),则该双曲线的离心率等于
A  B
B
 C
C
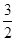 D
D
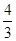
【解析】 C正确.
C正确.
科目:gzsx 来源:2012年普通高等学校招生全国统一考试天津卷数学文科 题型:022
已知双曲线C1:![]() -
-![]() =1(a>0,b>0)与双曲线C2:
=1(a>0,b>0)与双曲线C2:![]() -
-![]() =1有相同的渐近线,且C1的右焦点为F(
=1有相同的渐近线,且C1的右焦点为F(![]() ,0),则a=________b=________
,0),则a=________b=________
科目:gzsx 来源:江苏省南通市通州区2012届高三4月查漏补缺专项检测数学试题 题型:044
已知椭圆C:![]() +y2=1(a>1)的右焦点为F(c,o)(c>1),点P在圆O:x2+y2=1上任意一点(点P第一象限内),过点P作圆O的切线交椭圆C于两点Q、R.
+y2=1(a>1)的右焦点为F(c,o)(c>1),点P在圆O:x2+y2=1上任意一点(点P第一象限内),过点P作圆O的切线交椭圆C于两点Q、R.
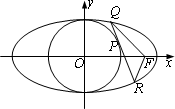
(1)证明:|PQ|+|FQ|=a;
(2)若椭圆离心率为![]() ,求线段QR长度的最大值.
,求线段QR长度的最大值.
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| FD |
| BF |
| FD |
| MP |
| MQ |
科目:gzsx 来源: 题型:
| x2 |
| 4 |
. |
| FA |
. |
| FB |
. |
| FC |
. |
| 0 |
. |
| FA |
. |
| FB |
. |
| FC |