精英家教网 >
试题搜索列表 >在四边形ABCD中,BC>BA,AD=DC,BD平分∠ABC,试猜想∠A与∠C有什么关系?并证明理由
在四边形ABCD中,BC>BA,AD=DC,BD平分∠ABC,试猜想∠A与∠C有什么关系?并证明理由答案解析
科目:czsx
来源:
题型:
已知在四边形ABCD中,BC>AB AD=DC,BD平分∠ABC 求证:∠A+∠C=18Oº
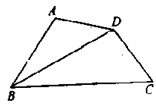
查看答案和解析>>
科目:czsx
来源:
题型:
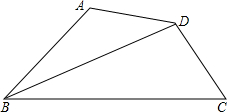
如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,
求证:∠A+∠C=180°.
查看答案和解析>>
科目:czsx
来源:
题型:
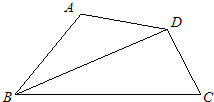
13、如图所示,在四边形ABCD中,BC>BA,AD=DC,BD平分∠ABC,则∠A+∠C的度数是
180
度.
查看答案和解析>>
科目:czsx
来源:
题型:

已知:在四边形ABCD中,BC>BA,∠A+∠C=180°,且∠C=60°,BD平分∠ABC,求证:BC=AB+DC.
查看答案和解析>>
科目:czsx
来源:
题型:
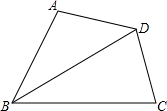
如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,
(1)分别作出D到BA、BC的距离DE、DF;
(2)求证:∠A+∠C=180°.
查看答案和解析>>
科目:czsx
来源:《第29章 几何的回顾》2010年单元综合检测B卷(解析版)
题型:填空题
如图所示,在四边形ABCD中,BC>BA,AD=DC,BD平分∠ABC,则∠A+∠C的度数是
度.

查看答案和解析>>
科目:czsx
来源:69领航·单元同步训练 八年级(上册) 数学(人教版)
题型:022
如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,则∠A+∠C=________.
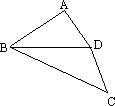
查看答案和解析>>
科目:czsx
来源:学习周报 数学 北师大九年级版 2009-2010学年 第2期 总第158期 北师大版
题型:047
已知:如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC.
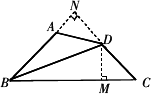
求证:∠A+∠C=180°.
查看答案和解析>>
科目:czsx
来源:
题型:047
已知,如图,在四边形 ABCD 中,BC>BA,AD=DC,BD 平分 ∠ABC.求证:∠A+∠C=180°.
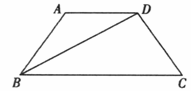
查看答案和解析>>
科目:czsx
来源:走向清华北大·初二数学
题型:044
如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,求∠ABC+∠ADC的度数.

查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,
求证:∠A+∠C=180°.
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
已知:在四边形ABCD中,BC>BA,∠A+∠C=180°,且∠C=60°,BD平分∠ABC,求证:BC=AB+DC.
查看答案和解析>>
科目:czsx
来源:浙江省同步题
题型:证明题
如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,求证:∠A+∠C=180°.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
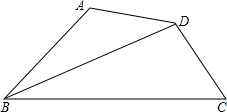 如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,
如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,
求证:∠A+∠C=180°.
查看答案和解析>>
科目:czsx
来源:新课标 读想练同步测试 七年级数学(下) 北师大版
题型:047
如图所示,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC.求证:∠A+∠C= .
.

查看答案和解析>>
科目:czsx
来源:
题型:
如图,在四边形ABCD中,BC>BA,AD=DC,BD平分∠ABC.
求 证:∠BAD+∠C=180°.
证:∠BAD+∠C=180°.
查看答案和解析>>
科目:czsx
来源:
题型:填空题
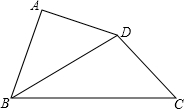 如图所示,在四边形ABCD中,BC>BA,AD=DC,BD平分∠ABC,则∠A+∠C的度数是________度.
如图所示,在四边形ABCD中,BC>BA,AD=DC,BD平分∠ABC,则∠A+∠C的度数是________度.
查看答案和解析>>
科目:czsx
来源:
题型:
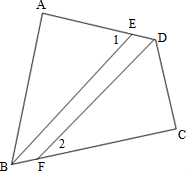
如图在四边形ABCD中,∠A=∠C=90度,BE平分∠ABC,DF平分∠ADC,
(1)∠1与∠2有什么关系?说明理由.
(2)BE与DF有什么位置关系?说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
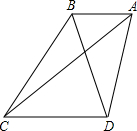
如图,四边形ABCD中,AB∥CD,AD=DC=BD=3,BC=4,则AC=
.
查看答案和解析>>
科目:czsx
来源:2011-2012年湖北宜昌市长阳县八年级上期末复习(一)数学试卷(带解析)
题型:解答题
如图,在梯形ABCD中,AB∥CD,∠BCD=90°, BD平分∠ABC
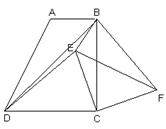
求证:(1) DC=BC;
(2) E是梯形内一点,F是梯形外一点,且∠EDC=∠FBC,DE=BF,试判断△ECF的形状,并证明你的结论;
(3) 在(2)的条件下,当BE:CE=1:2,∠BEC=135°时,求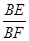 的值.
的值.
查看答案和解析>>

 如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,
如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,


![]() .
.
 如图在四边形ABCD中,∠A=∠C=90度,BE平分∠ABC,DF平分∠ADC,
如图在四边形ABCD中,∠A=∠C=90度,BE平分∠ABC,DF平分∠ADC,
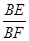 的值.
的值.