
题目列表(包括答案和解析)
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分12分)
已知函数 .
.
(I)求函数 的最小正周期;
的最小正周期;
(Ⅱ)当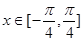 时,函数
时,函数 的最小值为
的最小值为 ,求实数
,求实数 的值.
的值.
三.解答题(解答应写出文字说明,证明过程或演算步骤):
17. (本小题满分12分)
已知等比数列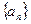 中,
中,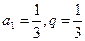 ,
,
(1)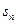 为数列
为数列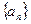 前
前 项的和,证明:
项的和,证明:
(2)设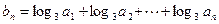 ,求数列
,求数列 的通项公式;
的通项公式;
(17) (本小题满分12分)在△ABC中,BC=2![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求AB的值;w.w.(Ⅱ)求![]() 的值.
的值.
17(本小题满分12分)
设等差数列![]() 满足
满足![]() ,
,![]() 。
。
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)求![]() 的前
的前![]() 项和
项和![]() 及使得
及使得![]() 最大的序号
最大的序号![]() 的值。
的值。
(本小题满分12分)
某市为了对学生的数理(数学与物理)学习能力进行分析,从10000名学生中随机抽出100位学生的数理综合学习能力等级分数(6分制)作为样本,分数频数分布如下表:
|
等级得分 |
|
|
|
|
|
|
|
人数 |
3 |
17 |
30 |
30 |
17 |
3 |
(Ⅰ)如果以能力等级分数大于4分作为良好的标准,从样本中任意抽取2名学生,求恰有1名学生为良好的概率;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值(例如区间 的中点值为1.5)作为代表:
的中点值为1.5)作为代表:
(ⅰ)据此,计算这100名学生数理学习能力等级分数的期望 及标准差
及标准差 (精确到0.1);
(精确到0.1);
(ⅱ) 若总体服从正态分布,以样本估计总体,估计该市这10000名学生中数理学习能力等级在 范围内的人数 .
范围内的人数 .
(Ⅲ)从这10000名学生中任意抽取5名同学,
他们数学与物理单科学习能力等级分
数如下表:


(ⅰ)请画出上表数据的散点图;
(ⅱ)请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程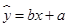 (附参考数据:
(附参考数据: )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com