某港口水的深度y(米)是时间t(0≤t≤24，单位：时)的函数，记作y＝f(t)，下面是某日水深的数据：

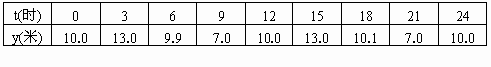
经长期观察，y＝f(t)的曲线可近似地看成函数y＝Asinωt＋b的图象．

(Ⅰ)试根据以上数据，求出函数y＝Asinωt＋b的最小正周期、振幅和表达式；

(Ⅱ)一般情况下，船舶航行时，船底离海底的距离为5米或5米以上时认为是安全的(船舶停靠时，船底只需不碰海底即可)，某船吃水深度(船底离水面的距离)为6.5米，如果该船希望在同一天内安全进出港，请问，它至多能在港内停留多长时间(忽略进出港所需的时间)．

某港口的水深y(米)是时间t(，单位：小时)的函数，下面是水深的数据：

根据上述数据描出的曲线如下图所示，经拟合，该曲线可近似地看成正弦函数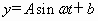的图象．

(1)试根据以上数据，求出的表达式；

(2)一般情况下，船舶航行时，般底离海底的距离不少于4.5米时是安全的，如果某般的吃水深度(般底与水面的距离)为7米，那么该般在什么时间段能够安全进港?若该般欲当天安全离港，则在港内停留的时间最多不能超过多长时间(忽略进出港所用的时间)？

经长期观察，y=f(t)的曲线可以近似地看成函数y=Asinωx+b的图象.

（1）试根据以上数据，求出函数y=f(t)的近似表达式；

（2）一般情况下，船舶航行时，船底离海底的距离为5米或5米以上时认为是安全的（船舶停靠时，船底只需不碰海底即可）.某船吃水深度（船底离水面的距离）为6.5米.如果该船希望在同一天内安全进出港，请问，它至多能在港内停留多长时间（忽略进出港时间）？