
题目列表(包括答案和解析)
14.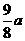 .因为点P是AB的中点,由垂径定理知,
.因为点P是AB的中点,由垂径定理知, 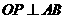 .
.
在 中,
中,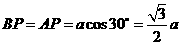 .由相交线定理知,
.由相交线定理知,
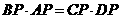 ,即
,即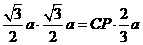 ,所以
,所以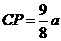 .[来源:KS5
.[来源:KS5
15.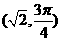 .由极坐标方程与普通方程的互化式
.由极坐标方程与普通方程的互化式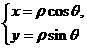 知,这两条曲线的普通方程分别为
知,这两条曲线的普通方程分别为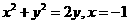 .解得
.解得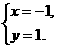 由
由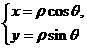 得点(-1,1)的极坐标为
得点(-1,1)的极坐标为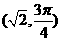 .[来源
.[来源
(2010广东理数)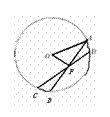 14、(几何证明选讲选做题)如图3,AB,CD是半径为a的圆O的两条弦,它们相交于AB的中点P,PD=
14、(几何证明选讲选做题)如图3,AB,CD是半径为a的圆O的两条弦,它们相交于AB的中点P,PD=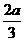 ,∠OAP=30°,则CP=______.
,∠OAP=30°,则CP=______.
15、(2010广东理数)(坐标系与参数方程选做题)在极坐标系(ρ,θ)(0 ≤ θ<2π)中,曲线ρ=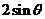 与
与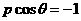 的交点的极坐标为______.
的交点的极坐标为______.
15.(2010陕西文数)(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
A.(不等式选做题)不等式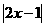 <3的解集为
<3的解集为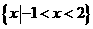 .
.
解析: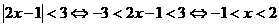
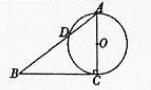 B.(几何证明选做题)如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则BD=
B.(几何证明选做题)如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则BD=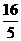 cm.
cm.
解析: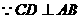 ,由直角三角形射影定理可得
,由直角三角形射影定理可得
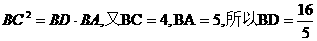
C.(坐标系与参数方程选做题)参数方程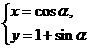 (
(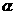 为参数)化成普通方程为
为参数)化成普通方程为
x2+(y-1)2=1.
解析: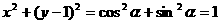
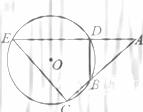 (2010北京理数)(12)如图,
(2010北京理数)(12)如图, 的弦ED,CB的延长线交于点A。若BD
的弦ED,CB的延长线交于点A。若BD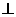 AE,AB=4, BC=2, AD=3,则DE=
;CE=
。
AE,AB=4, BC=2, AD=3,则DE=
;CE=
。
答案:5 
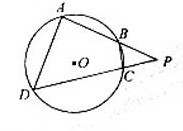 (2010天津文数)(11)如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P。若PB=1,PD=3,则
(2010天津文数)(11)如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P。若PB=1,PD=3,则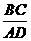 的值为 。
的值为 。
[答案]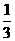
[解析]本题主要考查四点共圆的性质与相似三角形的性质,属于容易题。
因为A,B,C,D四点共圆,所以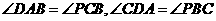 ,因为
,因为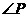 为公共角,所以
为公共角,所以
⊿PBC∽⊿PAB,所以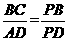 =
=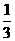
[温馨提示]四点共圆时四边形对角互补,圆与三角形综合问题是高考中平面几何选讲的重要内容,也是考查的热点。
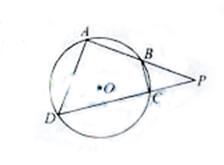 (2010天津理数)(14)如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P,若
(2010天津理数)(14)如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P,若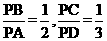 ,则
,则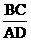 的值为 。
的值为 。
[答案]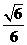
[解析]本题主要考查四点共圆的性质与相似三角形的性质,属于中等题。
因为A,B,C,D四点共圆,所以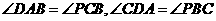 ,因为
,因为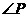 为公共角,所以
为公共角,所以
⊿PBC∽⊿PAB,所以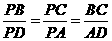 .设OB=x,PC=y,则有
.设OB=x,PC=y,则有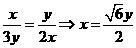 ,所以
,所以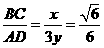
[温馨提示]四点共圆时四边形对角互补,圆与三角形综合问题是高考中平面几何选讲的重要内容,也是考查的热点。
(2010天津理数)(13)已知圆C的圆心是直线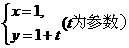 与x轴的交点,且圆C与直线x+y+3=0相切,则圆C的方程为
与x轴的交点,且圆C与直线x+y+3=0相切,则圆C的方程为
[答案]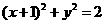
本题主要考查直线的参数方程,圆的方程及直线与圆的位置关系等基础知识,属于容易题。
令y=0得t=-1,所以直线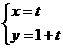 与x轴的交点为(-1.0)
与x轴的交点为(-1.0)
因为直线与圆相切,所以圆心到直线的距离等于半径,即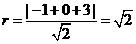 ,所以圆C的方程为
,所以圆C的方程为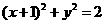
[温馨提示]直线与圆的位置关系通常利用圆心到直线的距离或数形结合的方法求解。
3.(2010上海文数)行列式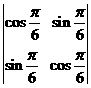 的值是 0.5 。
的值是 0.5 。
解析:考查行列式运算法则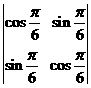 =
=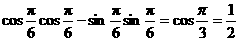
3.(2010江苏卷)6、在平面直角坐标系xOy中,双曲线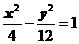 上一点M,点M的横坐标是3,则M到双曲线右焦点的距离是___▲_______
上一点M,点M的横坐标是3,则M到双曲线右焦点的距离是___▲_______
[解析]考查双曲线的定义。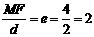 ,
,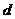 为点M到右准线
为点M到右准线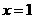 的距离,
的距离,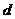 =2,MF=4。
=2,MF=4。
15.(2010湖北文数)已知椭圆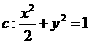 的两焦点为
的两焦点为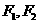 ,点
,点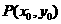 满足
满足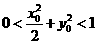 ,则|
,则|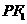 |+
|+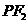 |的取值范围为_______,直线
|的取值范围为_______,直线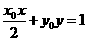 与椭圆C的公共点个数_____。
与椭圆C的公共点个数_____。
[答案]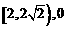
[解析]依题意知,点P在椭圆内部.画出图形,由数形结合可得,当P在原点处时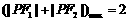 ,当P在椭圆顶点处时,取到
,当P在椭圆顶点处时,取到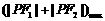 为
为
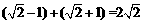 ,故范围为
,故范围为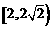 .因为
.因为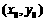 在椭圆
在椭圆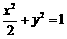 的内部,则直线
的内部,则直线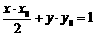 上的点(x, y)均在椭圆外,故此直线与椭圆不可能有交点,故交点数为0个.
上的点(x, y)均在椭圆外,故此直线与椭圆不可能有交点,故交点数为0个.
16. 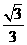 [命题意图]本小题主要考查椭圆的方程与几何性质、第二定义、平面向量知识,考查了数形结合思想、方程思想,本题凸显解析几何的特点:“数研究形,形助数”,利用几何性质可寻求到简化问题的捷径.
[命题意图]本小题主要考查椭圆的方程与几何性质、第二定义、平面向量知识,考查了数形结合思想、方程思想,本题凸显解析几何的特点:“数研究形,形助数”,利用几何性质可寻求到简化问题的捷径.
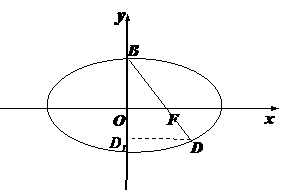 [解析1]如图,
[解析1]如图,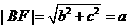 ,
,
作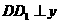 轴于点D1,则由
轴于点D1,则由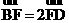 ,得
,得
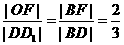 ,所以
,所以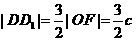 ,
,
即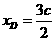 ,由椭圆的第二定义得
,由椭圆的第二定义得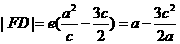
又由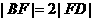 ,得
,得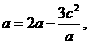
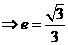
[解析2]设椭圆方程为第一标准形式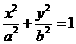 ,设
,设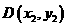 ,F分 BD所成的比为2,
,F分 BD所成的比为2,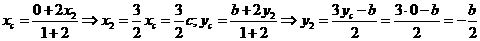 ,代入
,代入
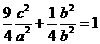 ,
,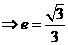
(2010全国卷1理数)

13.(2010福建文数) 若双曲线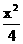 -
-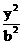 =1(b>0)的渐近线方程式为y=
=1(b>0)的渐近线方程式为y=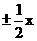 ,则b等于 。
,则b等于 。
[答案]1
[解析]由题意知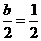 ,解得b=1。
,解得b=1。
[命题意图]本小题考查双曲线的几何性质、待定系数法,属基础题。
(2010全国卷1文数)(16)已知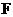 是椭圆
是椭圆 的一个焦点,
的一个焦点,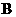 是短轴的一个端点,线段
是短轴的一个端点,线段 的延长线交
的延长线交 于点
于点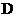 , 且
, 且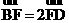 ,则
,则 的离心率为
.
的离心率为
.
15.(2010江西理数)点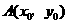 在双曲线
在双曲线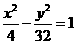 的右支上,若点A到右焦点的距离等于
的右支上,若点A到右焦点的距离等于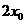 ,则
,则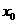 =
=
[答案] 2
[解析]考查圆锥曲线的基本概念和第二定义的转化,读取a=2.c=6,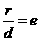
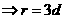 ,
,
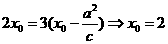
(2010安徽文数)(12)抛物线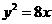 的焦点坐标是
的焦点坐标是
答案: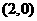
[解析]抛物线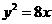 ,所以
,所以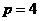 ,所以焦点
,所以焦点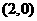 .
.
[误区警示]本题考查抛物线的交点.部分学生因不会求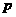 ,或求出
,或求出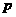 后,误认为焦点
后,误认为焦点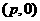 ,还有没有弄清楚焦点位置,从而得出错误结论.
,还有没有弄清楚焦点位置,从而得出错误结论.
(2010重庆文数) (13)已知过抛物线
(13)已知过抛物线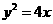 的焦点
的焦点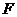 的直线交该抛物线于
的直线交该抛物线于 、
、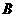 两点,
两点,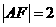 ,则
,则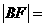 ____________ .
____________ .
解析:由抛物线的定义可知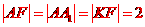
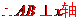 故
故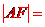
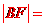 2
2
(2010重庆理数)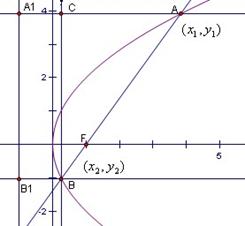 (14)已知以F为焦点的抛物线
(14)已知以F为焦点的抛物线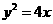 上的两点A、B满足
上的两点A、B满足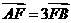 ,则弦AB的中点到准线的距离为___________.
,则弦AB的中点到准线的距离为___________.
解析:设BF=m,由抛物线的定义知
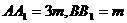
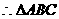 中,AC=2m,AB=4m,
中,AC=2m,AB=4m,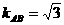
直线AB方程为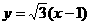
与抛物线方程联立消y得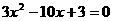
所以AB中点到准线距离为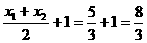
(2010北京文数)(13)已知双曲线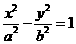 的离心率为2,焦点与椭圆
的离心率为2,焦点与椭圆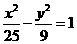 的焦点相同,那么双曲线的焦点坐标为
;渐近线方程为 。
的焦点相同,那么双曲线的焦点坐标为
;渐近线方程为 。
答案:(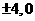 )
) 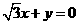
(2010北京理数)(13)已知双曲线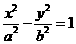 的离心率为2,焦点与椭圆
的离心率为2,焦点与椭圆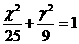 的焦点相同,那么双曲线的焦点坐标为 ;渐近线方程为
。
的焦点相同,那么双曲线的焦点坐标为 ;渐近线方程为
。
答案:(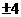 ,0)
,0) 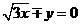
(2010天津文数)(13)已知双曲线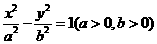 的一条渐近线方程是
的一条渐近线方程是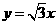 ,它的一个焦点与抛物线
,它的一个焦点与抛物线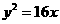 的焦点相同。则双曲线的方程为
。
的焦点相同。则双曲线的方程为
。
[答案]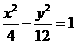
[解析]本题主要考查了双曲线和抛物线的几何性质及双曲线的标准方程,属于容易题。
由渐近线方程可知 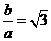 ①
①
因为抛物线的焦点为(4,0),所以c=4 ②
又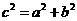 ③
③
联立①②③,解得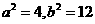 ,所以双曲线的方程为
,所以双曲线的方程为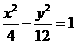
[温馨提示]求圆锥曲线的标准方程通常利用待定洗漱法求解,注意双曲线中c最大。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com