10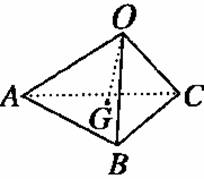．如图已知点G是△ABC的重心，O是空间任一点，若++＝λ，则λ的值是________．

答案：3

解析：如图G为重心，E为AB的中点

＝(+)，

＝＝(－)，

＝+＝+(－)＝(++)，

∴λ＝3.

9．在四面体O－ABC中，＝a，＝b，＝c，D为BC的中点，E为AD的中点，则＝________(用a、b、c表示)．

答案：a+b+c

命题意图：考查空间向量基本定理的应用．

解析：＝+＝a+＝a+(－)

＝a+＝a+×(+)

＝a+b+c，

故填a+b+c.

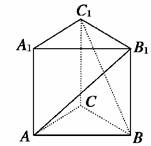
8．在正三棱柱ABC－A₁B₁C₁中，若AB＝BB₁，则AB₁与C₁B所成的角的大小为　 (　)

A．60°　 B．90°　 C．105°　 D．75°

答案：B

解析：如下图，＝+

＝+，设||＝1，

∴·＝·+·+·+·＝··cos120°+1＝0.

∴AB₁⊥BC₁.

7．如图，空间四边形OABC中，＝a，＝b，＝c，点M在OA上，且OM＝2MA，N为BC中点，则等于　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

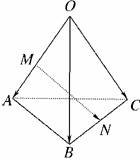
A.a－b+c　　　　 B．－a+b+c

C.a+b－c　　　　 D.a+b－c

答案：B

解析：∵＝－＝(+)－＝(b+c)－a＝－a+b+c.

故选B.

6．已知空间四边形ABCD每边及对角线长均为，E、F、G分别是AB、AD、DC的中点，则·等于　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

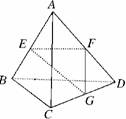
A. 　　　　　　　　　　 　B．1 　　　　　　　　 C. 　　　　　　　　　 　D.

答案：A

解析：由于ABCD为正四面体，E、F、G为中点，因此△EFG为等腰直角三角形，所以·＝

||·||·cos45°＝1××＝.故选A.

5．若A、B、C、D是空间不共面的四点，且满足·＝0，·＝0，·＝0，则△BCD是　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．钝角三角形　 B．锐角三角形　　 C．直角三角形 　　　　 D．不确定

答案：B

解析：∵·＝(－)·(－)＝·－·－·+²>0，同理·>0，·>0，故△BCD为锐角三角形．因此选B.

4．对于空间任意一点O和不共线的三点A、B、C，若＝x+y+z(其中x、y、z∈R)，则x+y+z＝1是四点P、A、B、C共面的　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．必要而不充分条件　　　 B．充分而不必要条件

C．充要条件　　　　　　　 D．既不充分也不必要条件

答案：C

解析：若四点P，A，B，C共面，根据共面定理知：

＝λ+ω(λ，ω∈R)，

∴－＝λ(－)+ω(－)，

＝(1－λ－ω)+λ+ω，

令x＝1－λ－ω，y＝λ，z＝ω，

即＝x+y+z，且

x+y+z＝1.

反之，若x+y+z＝1，则x＝1－y－z，代入已知条件得

＝(1－y－z)+y+z，

于是－＝y(－)+z(－)，

即＝y+z，

由共面向量定理知P、A、B、C四点共面．

3．已知空间四边形ABCD，连结AC、BD，设M、G分别是BC、CD的中点，则+(+)等于　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

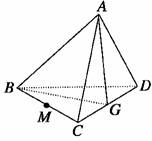
A.　 B.　 C.　 D.

答案：A

解析：如图所示，+(+)＝+＝.

2．已知A、B、C三点不共线，点O是平面ABC外一点，则在下列各条件中，能得到点M与A、B、C一定共面的条件为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.＝++　　　 B.＝－+

C.＝++　　　　 D.＝2－－

答案：B

解析：由共面向量定理的推论知、、的系数之和为1，选项B中+(－)+1＝1符合．

1．在空间四点O、A、B、C中，若O、O、O是空间的一个基底，则下列命题中，不正确的是　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．O、A、B、C四点不共线　　　 B．O、A、B、C四点共面，但不共线

C．O、A、B、C四点不共面　　　 D．O、A、B、C四点中任三点不共线

答案：B