
题目列表(包括答案和解析)
 (选做题)在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
(选做题)在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.| 3 |
| 3 |
|
| 2 |
| π |
| 4 |
|
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
(本小题满分16分)
对于函数y=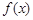 ,x∈(0,
,x∈(0,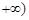 ,如果a,b,c是一个三角形的三边长,那么
,如果a,b,c是一个三角形的三边长,那么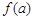 ,
,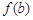 ,
,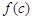 也是一个三角形的三边长, 则称函数
也是一个三角形的三边长, 则称函数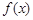 为“保三角形函数”.
为“保三角形函数”.
对于函数y=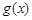 ,x∈
,x∈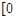 ,
,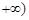 ,如果a,b,c是任意的非负实数,都有
,如果a,b,c是任意的非负实数,都有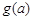 ,
,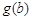 ,
,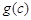 是一个三角形的三边长,则称函数
是一个三角形的三边长,则称函数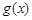 为“恒三角形函数”.
为“恒三角形函数”.
(1)判断三个函数“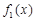 =x,
=x,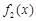 =
=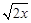 ,
,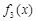 =
=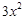 (定义域均为x∈(0,
(定义域均为x∈(0,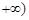 )”中,那些是“保三角形函数”?请说明理由;
)”中,那些是“保三角形函数”?请说明理由;
(2)若函数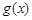 =
=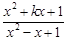 ,x∈
,x∈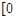 ,
,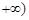 是“恒三角形函数”,试求实数k的取值范围;
是“恒三角形函数”,试求实数k的取值范围;
(3)如果函数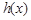 是定义在(0,
是定义在(0,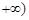 上的周期函数,且值域也为(0,
上的周期函数,且值域也为(0,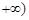 ,试证明:
,试证明: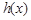 既不是“恒三角形函数”,也不是“保三角形函数”.
既不是“恒三角形函数”,也不是“保三角形函数”.
(本小题满分16分)
对于函数y=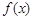 ,x∈(0,
,x∈(0,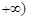 ,如果a,b,c是一个三角形的三边长,那么
,如果a,b,c是一个三角形的三边长,那么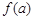 ,
,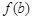 ,
,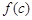 也是一个三角形的三边长, 则称函数
也是一个三角形的三边长, 则称函数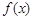 为“保三角形函数”.
为“保三角形函数”.
对于函数y=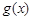 ,x∈
,x∈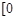 ,
,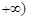 ,如果a,b,c是任意的非负实数,都有
,如果a,b,c是任意的非负实数,都有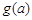 ,
,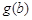 ,
,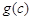 是一个三角形的三边长,则称函数
是一个三角形的三边长,则称函数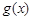 为“恒三角形函数”.
为“恒三角形函数”.
(1)判断三个函数“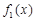 =x,
=x,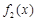 =
=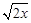 ,
,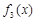 =
=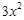 (定义域均为x∈(0,
(定义域均为x∈(0,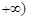 )”中,那些是“保三角形函数”?请说明理由;
)”中,那些是“保三角形函数”?请说明理由;
(2)若函数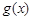 =
=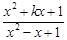 ,x∈
,x∈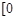 ,
,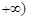 是“恒三角形函数”,试求实数k的取值范围;
是“恒三角形函数”,试求实数k的取值范围;
(3)如果函数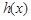 是定义在(0,
是定义在(0,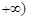 上的周期函数,且值域也为(0,
上的周期函数,且值域也为(0,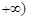 ,试证明:
,试证明: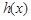 既不是“恒三角形函数”,也不是“保三角形函数”.
既不是“恒三角形函数”,也不是“保三角形函数”.
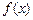 ,x∈(0,
,x∈(0, ,如果a,b,c是一个三角形的三边长,那么
,如果a,b,c是一个三角形的三边长,那么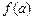 ,
,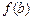 ,
,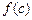 也是一个三角形的三边长, 则称函数
也是一个三角形的三边长, 则称函数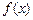 为“保三角形函数”.
为“保三角形函数”. ,x∈
,x∈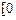 ,
, ,如果a,b,c是任意的非负实数,都有
,如果a,b,c是任意的非负实数,都有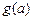 ,
,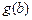 ,
,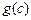 是一个三角形的三边长,则称函数
是一个三角形的三边长,则称函数 为“恒三角形函数”.
为“恒三角形函数”.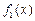 =x,
=x, =
=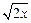 ,
,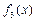 =
=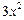 (定义域均为x∈(0,
(定义域均为x∈(0, )”中,那些是“保三角形函数”?请说明理由;
)”中,那些是“保三角形函数”?请说明理由; =
=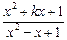 ,x∈
,x∈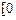 ,
, 是“恒三角形函数”,试求实数k的取值范围;
是“恒三角形函数”,试求实数k的取值范围; 是定义在(0,
是定义在(0, 上的周期函数,且值域也为(0,
上的周期函数,且值域也为(0, ,试证明:
,试证明: 既不是“恒三角形函数”,也不是“保三角形函数”.
既不是“恒三角形函数”,也不是“保三角形函数”.设椭圆 的中心和抛物线
的中心和抛物线 的顶点均为原点
的顶点均为原点 ,
, 、
、 的焦点均在
的焦点均在 轴上,过
轴上,过 的焦点F作直线
的焦点F作直线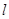 ,与
,与 交于A、B两点,在
交于A、B两点,在 、
、 上各取两个点,将其坐标记录于下表中:
上各取两个点,将其坐标记录于下表中: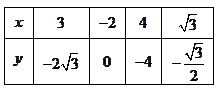

(1)求 ,
, 的标准方程;
的标准方程;
(2)若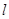 与
与 交于C、D两点,
交于C、D两点,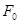 为
为 的左焦点,求
的左焦点,求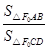 的最小值;
的最小值;
(3)点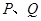 是
是 上的两点,且
上的两点,且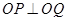 ,求证:
,求证: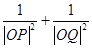 为定值;反之,当
为定值;反之,当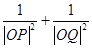 为此定值时,
为此定值时,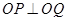 是否成立?请说明理由.
是否成立?请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com