
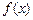 ,x∈(0,
,x∈(0, ,如果a,b,c是一个三角形的三边长,那么
,如果a,b,c是一个三角形的三边长,那么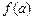 ,
,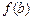 ,
,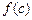 也是一个三角形的三边长, 则称函数
也是一个三角形的三边长, 则称函数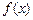 为“保三角形函数”.
为“保三角形函数”. ,x∈
,x∈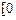 ,
, ,如果a,b,c是任意的非负实数,都有
,如果a,b,c是任意的非负实数,都有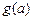 ,
,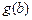 ,
,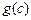 是一个三角形的三边长,则称函数
是一个三角形的三边长,则称函数 为“恒三角形函数”.
为“恒三角形函数”.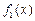 =x,
=x, =
=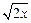 ,
,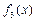 =
=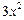 (定义域均为x∈(0,
(定义域均为x∈(0, )”中,那些是“保三角形函数”?请说明理由;
)”中,那些是“保三角形函数”?请说明理由; =
=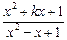 ,x∈
,x∈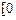 ,
, 是“恒三角形函数”,试求实数k的取值范围;
是“恒三角形函数”,试求实数k的取值范围; 是定义在(0,
是定义在(0, 上的周期函数,且值域也为(0,
上的周期函数,且值域也为(0, ,试证明:
,试证明: 既不是“恒三角形函数”,也不是“保三角形函数”.
既不是“恒三角形函数”,也不是“保三角形函数”.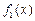 =x,它在(0,
=x,它在(0, 上是增函数,不妨设a≤b≤c,则
上是增函数,不妨设a≤b≤c,则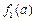 ≤
≤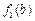 ≤
≤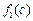 ,因为a+b>c,所以
,因为a+b>c,所以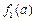 +
+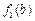 =a+b>c=
=a+b>c=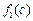 ,故
,故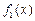 是“保三角形函数”.
是“保三角形函数”. =
=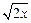 ,它在(0,
,它在(0, 上是增函数,,不妨设a≤b≤c,则
上是增函数,,不妨设a≤b≤c,则 ≤
≤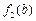 ≤
≤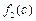 ,因为a+b>c,所以
,因为a+b>c,所以 +
+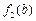 =
=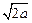 +
+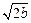 =
=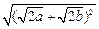 >
>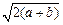 >
>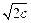 =
=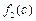 ,故
,故 是“保三角形函数”.
是“保三角形函数”.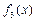 =
=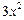 ,取a=3,b=3,c=5,显然a,b,c是一个三角形的三边长,但因为
,取a=3,b=3,c=5,显然a,b,c是一个三角形的三边长,但因为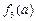 +
+ =
=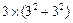 <
<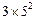 =
=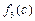 ,所以
,所以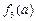 ,
, ,
,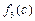 不是三角形的三边长,故
不是三角形的三边长,故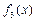 不是“保三角形函数”.
不是“保三角形函数”. =1+
=1+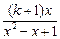 ,所以当x=0时,
,所以当x=0时, =1;当x>0时,
=1;当x>0时, =1+
=1+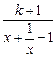 .
. =1,适合题意.
=1,适合题意. =1+
=1+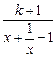 ≤1+
≤1+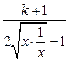 =k+2,所以
=k+2,所以 ∈
∈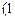 ,
,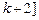 .从而当k>
.从而当k>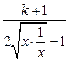 -1时,
-1时, ∈
∈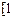 ,
,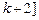 .由1+1>k+2,得k<0,所以-1<k<0.
.由1+1>k+2,得k<0,所以-1<k<0. =1+
=1+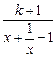 ≥1+
≥1+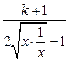 =k+2,所以
=k+2,所以 ∈
∈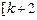 ,
,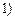 ,从而当k>-1时,所以
,从而当k>-1时,所以 ∈
∈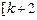 ,
, .由
.由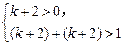 得,k>
得,k>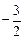 ,所以
,所以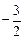 <k<-1.
<k<-1.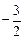 ,0).
,0).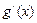 =
=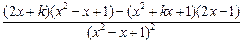 =
=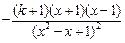 ,
, =1,适合题意.
=1,适合题意. 在
在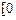 ,
,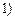 上单调递增,在
上单调递增,在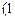 ,
, 上单调递减,而
上单调递减,而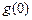 =1,
=1, =k+2,且当x>1时,
=k+2,且当x>1时, >1,所以此时
>1,所以此时 ∈
∈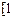 ,
,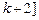 .
. 在
在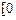 ,
,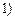 上单调递减,在
上单调递减,在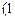 ,
, 上单调递增,而
上单调递增,而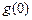 =1,
=1, =k+2,且当x>1时,
=k+2,且当x>1时, <1,所以此时
<1,所以此时 ∈
∈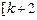 ,
, .
. 的值域是(0,
的值域是(0, ,所以存在正实数a,b,c,使得
,所以存在正实数a,b,c,使得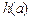 =1,
=1,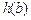 =1,
=1,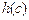 =2,显然这样的
=2,显然这样的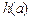 ,
,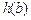 ,
,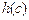 不是一个三角形的三边长.
不是一个三角形的三边长. 不是“恒三角形函数”.
不是“恒三角形函数”. 的最小正周期为T(T>0),令a=b=m+kT,c=n,其中k∈
的最小正周期为T(T>0),令a=b=m+kT,c=n,其中k∈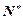 ,且k>
,且k>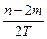 ,则a+b>c,又显然b+c>a,c+a>b,所以a,b,c是一个三角形的三边长.
,则a+b>c,又显然b+c>a,c+a>b,所以a,b,c是一个三角形的三边长.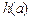 =
=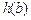 =
=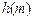 =1,
=1,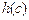 =
=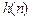 =2,所以
=2,所以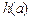 ,
,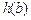 ,
,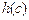 不是一个三角形的三边长.
不是一个三角形的三边长. 也不是“保三角形函数”.
也不是“保三角形函数”. 不是“保三角形函数”,然后根据此知
不是“保三角形函数”,然后根据此知 也不是“恒三角形函数”.)
也不是“恒三角形函数”.)

科目:高中数学 来源:不详 题型:单选题
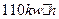 B.
B.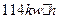 C.
C.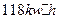 D.
D.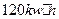
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com