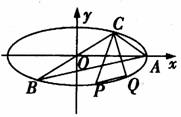（本小题满分14分）如图，已知A、B、C是长轴长为4的椭圆上的三点，点A是椭圆的右顶点，直线BC过椭圆的中心O（O为坐标原点），且.

  （1）求椭圆的标准方程；

  （2）如果椭圆上的两点P、Q，使得直线CP、CQ

与轴围成底边在轴上的等腰三角形，

是否总存在实数使得？

请给出证明.

（本小题满分14分）已知x，y之间的一组数据如下表： 

x	1	3	6	7	8
y	1	2	3	4	5

（1）以x为横坐标，y为纵坐标在直角坐标系中画出散点图，并说明这两个变量之间的关系是正相关关系还是负相关关系。
（2）求线性回归方程.

（本小题满分12分）（文题满分14分）

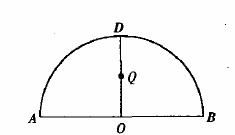
       如图，为半圆，AB为半圆直径，O为半圆圆心，且，Q为线段OD的中点，已知|AB|=4，曲线C过Q点，动点P在曲线C上运动且保持|PA|+|PB|的值不变。

   （Ⅰ）建立适当的平面直角坐标系，求曲线C的方程；

   （Ⅱ）过点B的直线与曲线C交于M、N两点，与OD所在直线交于E点，若为定值。

（本题满分14分）已知，，

（1）若f(x)在处取得极值，试求c的值和f(x)的单调增区间；

（2）如右图所示，若函数的图象在连续光滑，试猜想拉格朗日中值定理：即一定存在使得？（用含有a,b,f(a),f(b)的表达式直接回答）

（3）利用（2）证明：函数y=g(x)图象上任意两点的连线斜率不小于2e-4.

 （本题是选做题，满分28分，请在下面四个题目中选两个作答，每小题14分，多做按前两题给分）

A．(选修4-1：几何证明选讲)

如图，△ABC是⊙O的内接三角形，PA是⊙O的切线，PB交AC于点E，交⊙O于点D，若PE＝PA，，PD＝1，BD＝8，求线段BC的长.

 

 

 

 

 

 

B．(选修4-2：矩阵与变换)

在直角坐标系中，已知椭圆，矩阵阵，，求在矩阵作用下变换所得到的图形的面积.

C．(选修4-4：坐标系与参数方程)

直线(为参数，为常数且)被以原点为极点，轴的正半轴为极轴，方程为的曲线所截，求截得的弦长.

D．(选修4-5：不等式选讲)

设，求证：.