
题目列表(包括答案和解析)
| e |
| 1 |
| 4 |
| e |
若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其公共定义域上的任意实数
对其公共定义域上的任意实数 都满足:
都满足: 和
和 恒成立,则称此直线
恒成立,则称此直线 为
为 和
和 的“隔离直线”.已知函数
的“隔离直线”.已知函数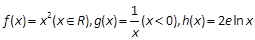 .有下列命题:
.有下列命题:
① 在
在 内单调递增;
内单调递增;
② 和
和 之间存在“隔离直线”, 且b的最小值为-4;
之间存在“隔离直线”, 且b的最小值为-4;
③ 和
和 之间存在“隔离直线”, 且k的取值范围是
之间存在“隔离直线”, 且k的取值范围是 ;
;
④ 和
和 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线” .
.
其中真命题的个数有( ).
| A.1个 | B.2个 | C.3个 | D.4个 |
 递减;
递减; ;
; .
. 和
和 ,使得函数
,使得函数 和
和 对其公共定义域上的任意实数
对其公共定义域上的任意实数 都满足:
都满足: 和
和 恒成立,则称此直线
恒成立,则称此直线 为
为 和
和 的“隔离直线”.已知函数
的“隔离直线”.已知函数 .有下列命题:
.有下列命题: 在
在 内单调递增;
内单调递增; 和
和 之间存在“隔离直线”, 且b的最小值为-4;
之间存在“隔离直线”, 且b的最小值为-4; 和
和 之间存在“隔离直线”, 且k的取值范围是
之间存在“隔离直线”, 且k的取值范围是 ;
; 和
和 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线” .
.| A.1个 | B.2个 | C.3个 | D.4个 |
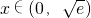 递减;
递减; ;
;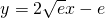 .
.一、选择题:
1.A 2.A 3.D 4.C
5.B 6.D 7.D 8.B
9.C 10.C 11.D 12.C
二、填空题:
13.-252
14. .files/image148.gif) 15. -3 16.
15. -3 16. .files/image150.gif) 17.
17..files/image152.gif)
三、解答题:
18解:(1).files/image154.gif)
.files/image156.gif)
(2)由题设,.files/image158.gif)
.files/image160.gif)
19解:(1)记“第一次与第二次取到的球上的号码的和是
.files/image162.gif)
所以第一次与第二次取到的地球上的号码的和是4的概率.files/image164.gif)
(2)记“第一次与第二次取到的上的号码的积不小于
.files/image166.gif)
|