（本小题满分12分）甲、乙两人玩数字游戏，先由甲任想一个数字记为a，再由乙猜甲刚才想的数字，把乙想的数字记为b，且
（I）求两人想的数字之差为3的概率；
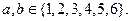
（II）若两人想的数字相同或相差1，则称“甲乙心有灵犀”，求“甲乙心有灵犀”的概率

查看答案和解析>>

查看答案和解析>>

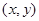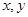（本小题满分12分）袋子中有质地、大小完全相同的4个球，编号分别为1，2，3，4．甲、乙两人玩一种游戏：甲先摸出一个球，记下编号，放回后乙再摸一个球，记下编号，若两个编号的和为奇数算甲赢，否则算乙赢．记基本事件为，其中分别为甲、乙摸到的球的编号。
（1）列举出所有的基本事件，并求甲赢且编号的和为5的事件发生的概率；
（2）比较甲胜的概率与乙胜的概率，并说明这种游戏规则是否公平。（无详细解答过程，不给分）
（3）  如果请你猜这两球的号码之和，猜中有奖．猜什么数获奖的可能性大？说明理由．

查看答案和解析>>

一．选择题：

1~5 ABDBC     6~10 ABDDC     11~12 BA

二．填空题：

13．     14．      15．     16．

三．解答题：

17．解：（1）  ，        ……1分

，                     ……2分

由 得

，

又 ，，                    ……5分

（2）由（1）知，，又C 为锐角，

                           ……10分

18．（1）记事件为甲出子，事件为乙猜对甲出子，

则，为相互独立的事件，记乙赢得1子的事件为

记三次游戏中甲获胜一次的事件为，则一次游戏中甲获胜的事件为，

则

(2)记乙获胜的事件为，则

=

甲获胜的概率大。

19．（1）证明：过作,分别交与

则分别为的中点，连接，

.则四边形是平行四边形

分别为的中点,平面

平面

(2)过作，垂足为，连接

则面

就是直线与面所成的角．

设，则

,直线与面所成的角是。

（3）由（2）时，

则,所以

又由（2）面，则

为二面角的平面角         

20．解（1）∵   无解 

   直线l与的图像不相切。                5分

      （2）由题意得;在x∈[-2,2]内恒成立

        即：    设

      ∵   ∴g(x) 在x∈[-2,2]内单调递增

∴g(x)的最大值为            12分

21．解：（1）证明：

   ，即

是以2为公比的等比数列

（2）解：，  ，

22．（1）设

       ,在线段的中垂线上

      ,又，则

又，

又

化简得即为的轨迹方程

（2）设直线

由          

又

由得