
题目列表(包括答案和解析)
(2007
北京崇文模拟)甲乙两人参加奥运知识竞赛,假设甲、乙两人答对每题的概率分别为 与
与 ,且答对一题得1分,答不对得0分.
,且答对一题得1分,答不对得0分.
(1)
甲、乙两人各答一题,求两人得分之和ξ的分布列及数学期望;(2)
甲、乙两人各答两题,每人每答一题记为一次,求这四次答题中至少有一次答对的概率.(本小题满分12分)对某班级50名同学一年来参加社会实践的次数进行的调查统计,得到如下频率分布表:
| 参加次数 | 0 | 1 | 2 | 3 |
| 人数 | 0.1 | 0.2 | 0.4 | 0.3 |
根据上表信息解答以下问题:
(Ⅰ)从该班级任选两名同学,用η表示这两人参加社会实践次数之和,记“函数![]() 在区间
在区间![]() ,
,![]() 内有零点”的事件为
内有零点”的事件为![]() ,求
,求![]() 发生的概率
发生的概率![]() ;
;
(Ⅱ)从该班级任选两名同学,用ξ表示这两人参加社会实践次数之差的绝对值,求随机变量ξ的分布列及数学期望Eξ.
对某班级50名同学一年来参加社会实践的次数进行的调查统计,得到如下频率分布表:
|
参加次数 |
0 |
1 |
2 |
3 |
|
人数 |
0.1 |
0.2 |
0.4 |
0.3 |
根据上表信息解答以下问题:
(1)从该班级任选两名同学,用η表示这两人参加社会实践次数之和,记“函数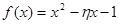 在区间
在区间 ,
,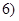 内有零点”的事件为
内有零点”的事件为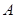 ,求
,求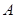 发生的概率
发生的概率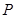 ;
;
(2)从该班级任选两名同学,用ξ表示这两人参加社会实践次数之差的绝对值,求随机变量ξ的分布列及数学期望Eξ
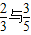 ,且答对一题得1分,答不对得0分.
,且答对一题得1分,答不对得0分.| 参加次数 | 0 | 1 | 2 | 3 |
| 人数 | 0.1 | 0.2 | 0.4 | 0.3 |
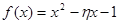 在区间
在区间 ,
, 内有零点”的事件为
内有零点”的事件为 ,求
,求 发生的概率
发生的概率 ;
;一、选择题(每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
C
A
B
B
C
C
D
D
D
A
A
二、填空题(每小题5分,共20分)
13. 14.
14.
 15. 1 16.
15. 1 16.

三、简答题
17.解:依题记“甲答对一题”为事件A ;“乙答对一题”为事件B
2分
则



∴ξ的分布列:
ξ
0
1
2
P



8分
∴ 10分
10分
18.解:当 时,原式
时,原式 3分
3分
当 时,有
时,有
∴原式= 7分
7分
当 时,
时,
∴原式 11分
11分
综上所述: 12分
12分
19.解:设切点( ),
), 3分
3分
∵切线与直线 平行
平行
∴

 或
或 10分
10分
∴切点坐标(1,-8)(-1,-12)
∴切线方程: 或
或
即: 或
或 12分
12分

21.解:设底面一边长为 ,则另一边长
,则另一边长
∴高为 3分
3分
由:
 ∴
∴
∵体积
 6分
6分
令 得
得 或
或 (舍去)
(舍去)
∵ 只有一个极值点
只有一个极值点
∴ ,此时高
,此时高 11分
11分
答:高为 12分
12分
22.解:假设 存在
存在
当 时,由
时,由 即:
即:
∴
当 时,
时, ∴
∴
猜想:
证明:1. 当 时,已证
时,已证
2. 假设 时结论成立
时结论成立

即为 时结论也成立
时结论也成立
由(1)(2)可知,对大于1的自然数n,存在 ,使
,使 成立 12分
成立 12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com