练习册

  • 练习册
  • 试题
    仅在点(3.0)处取得最大值.则a的取值范围为 . 【查看更多】

     

    题目列表(包括答案和解析)

    ．函数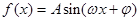 (其中A>0,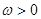,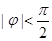)的图象如图所示，则，f(0)=       。

     

    查看答案和解析>>

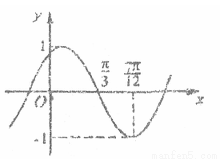
    （本小题满分14分）已知函数(其中A>0,)的图象如图所示.

    （1）求A，w及j的值；

    （2）若,求的值.

     

    查看答案和解析>>

    已知函数，其中a>0.

    （Ⅰ）求函数的单调区间；

    （Ⅱ）若直线是曲线的切线，求实数a的值；

    （Ⅲ）设，求在区间上的最大值（其中e为自然对的底数）。

     

    查看答案和解析>>

    已知函数f（x）= ,g（x）=3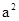lnx,其中a>0。若两曲线y=f（x）,y=g（x）有公共点，且在该点处的切线相同。则a的值为         。

    查看答案和解析>>

    已知某海滨浴场的海浪高度y（单位：米）与时间t（0≤t≤24）（单位：时）的函数关系记作y=f(t)，下表是某日各时的浪高数据：

    t（时）

    0

    3

    6

    9

    12

    15

    18

    21

    24

    y（米）

    1.5

    1.0

    0.5

    1.0

    1.5

    1.0

    0.5

    0.99

    1.5

    经长期观测，函数y=f(t)可近似地看成是函数。

    （1）根据以上数据，求出函数的最小正周期T及函数表达式（其中A>0，ω>0）；

    （2）根据规定，当海浪高度不低于0.75米时，才对冲浪爱好者开放，请根据以上结论，判断一天内从上午7时至晚上19时之间，该浴场有多少时间可向冲浪爱好者开放

    查看答案和解析>>

    1、C   2、B    3、C    4、D    5、C    6、B

    7、4       8、     9、  5       10、_2_

    11、【解】由得，

    又,所以, 

    当时，1<,即为真时实数的取值范围是1<.      …………2分

    由,得,即为真时实数的取值范围是. ……4分

    若为真，则真且真，

    所以实数的取值范围是.                       ……………………6分

    (Ⅱ) 是的充分不必要条件，即,且,   ……………8分

    设A=,B=,则,

    又A==, B==}， ……………10分

    则0<,且

    所以实数的取值范围是.                      ……………………12分

    12、【解】设公司在甲电视台和乙电视台做广告的时间分别为分钟和分钟，总收益为元，由题意得        ………………………………3分

    目标函数为．………5分

    二元一次不等式组等价于

    作出二元一次不等式组所表示的平面区域，即可行域．                ………………8分

    如图：作直线，

    即．

    平移直线，从图中可知，当直线过点时，目标函数取得最大值．   

    联立解得．

    点的坐标为．                       ………………………10分

    （元）

    答：该公司在甲电视台做100分钟广告，在乙电视台做200分钟广告，公司的收益最大，最大收益是70万元．                         …………………………12分

     

     

     

     


    同步练习册答案