
题目列表(包括答案和解析)
(本小题满分12分)设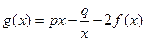 ,其中
,其中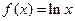 ,且
,且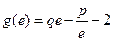 (
(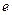 为自然对数的底)
为自然对数的底)
(1)求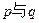 的关系;
的关系;
(2) 在其定义域内的单调函数,求
在其定义域内的单调函数,求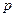 的取值范围;
的取值范围;
(3)求证:(i)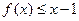
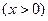
(ii)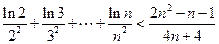 (
(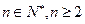 )。
)。
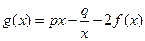 ,其中
,其中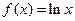 ,且
,且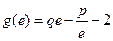 (
(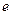 为自然对数的底)
为自然对数的底)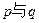 的关系;
的关系;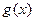 在其定义域内的单调函数,求
在其定义域内的单调函数,求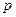 的取值范围;
的取值范围;
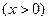
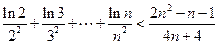 (
(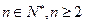 )。
)。 (本小题满分12分)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,
![]() ;(1)求数列
;(1)求数列![]() 的通项公式
的通项公式
(2)设数列![]() 满足:
满足:![]() ,且
,且![]() ,求证:
,求证:![]() (3)若(2)问中数列
(3)若(2)问中数列![]() 满足
满足 ![]() ,
,
求证: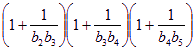
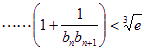 (其中
(其中![]() 为自然对数的底数)。
为自然对数的底数)。
(本小题满分14分)设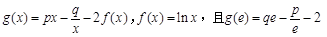 (e为自然对数的底)。
(e为自然对数的底)。
(1)求p与q的关系;
(2)若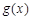 在其定义域为单调函数,求p的取值范围。
在其定义域为单调函数,求p的取值范围。
(3)证明: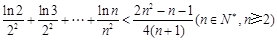 。
。
(本小题满分14分)已知函数 。
。
(1)求函数 的单调区间与最值;
的单调区间与最值;
(2)若方程 在区间
在区间 内有两个不相等的实根,求实数
内有两个不相等的实根,求实数 的取值范围; (其中e为自然对数的底数)
的取值范围; (其中e为自然对数的底数)
(3)如果函数 的图像与x轴交于两点
的图像与x轴交于两点 ,且
,且 ,求证:
,求证: (其中,
(其中, 是
是 的导函数,正常数
的导函数,正常数 满足
满足 )
)
一、选择题:
A卷:CCABD BDCBB AA
二、填空题:
(13).files/image339.gif) (14)
(14).files/image341.gif) (15)
(15).files/image343.gif) (16)
(16) .files/image345.gif)
三、解答题:
(17)解:
由.files/image238.gif) ,知
,知.files/image348.gif) ,又
,又.files/image236.gif) ,由正弦定理,有
,由正弦定理,有
.files/image351.gif) ,∴
,∴.files/image353.gif) ,
,.files/image355.gif) ,……3分
,……3分
∴.files/image357.gif) ……………5分
……………5分
.files/image359.gif)
.files/image361.gif) …………8分
…………8分
∵.files/image363.gif) ,
,.files/image365.gif) , ∴
, ∴.files/image367.gif) ,
,
故所求函数为.files/image369.gif)
.files/image371.gif) ,函数的值域为
,函数的值域为.files/image373.gif) ……………10分
……………10分
(18)解:
记顾客购买一件产品,获一等奖为事件.files/image375.gif) ,获二等奖为事件
,获二等奖为事件.files/image377.gif) ,不获奖为事件
,不获奖为事件.files/image379.gif) ,则
,则.files/image381.gif) ,
,.files/image383.gif) ,
,.files/image385.gif)
(Ⅰ)该顾客购买2件产品,中奖的概率
.files/image387.gif) ……………4分
……………4分
(Ⅱ).files/image188.gif) 的可能值为0,20,40,100,120,200,其中
的可能值为0,20,40,100,120,200,其中
.files/image390.gif) ,
,.files/image392.gif) ,
,
.files/image394.gif) ,
,.files/image396.gif) ,
,
.files/image398.gif) ,
,.files/image400.gif) ……………8分
……………8分
.files/image188.gif) 的分布列为
的分布列为
.files/image188.gif)
.files/image404.gif)
.files/image406.gif)
.files/image408.gif)
.files/image410.gif)
.files/image412.gif)
.files/image414.gif)
.files/image018.gif)
.files/image417.gif)
.files/image417.gif)
.files/image419.gif)
.files/image421.gif)
.files/image423.gif)
.files/image425.gif)
……………10分
.files/image188.gif) 的期望
的期望
.files/image427.gif)
.files/image429.gif) (元)…………………………………………………………………12分
(元)…………………………………………………………………12分
(19)解法一:
(Ⅰ)取.files/image431.gif) 中点
中点.files/image433.gif) ,连结
,连结.files/image435.gif) 、
、.files/image437.gif) ,则
,则.files/image439.gif) ,
,
又.files/image441.gif) ,
∴
,
∴.files/image443.gif) ,四边形
,四边形.files/image445.gif) 是平行四边形,
是平行四边形,
∴.files/image447.gif) ,又
,又.files/image449.gif) ,
,.files/image451.gif) ,
,
∴.files/image272.gif) ……………………………………………………4分
……………………………………………………4分
(Ⅱ)连结.files/image454.gif)
∵.files/image456.gif) , ∴
, ∴.files/image458.gif) ,
,
又平面.files/image460.gif) 平面
平面.files/image256.gif) ,∴
,∴.files/image463.gif)
而.files/image465.gif) , ∴
, ∴.files/image467.gif)
作.files/image469.gif) 于
于.files/image471.gif) ,则
,则.files/image473.gif) ,且
,且.files/image475.gif) ,
,.files/image471.gif) 为
为.files/image478.gif) 的中点。
的中点。
作.files/image480.gif) 于
于.files/image482.gif) ,连结
,连结.files/image484.gif) ,则
,则.files/image486.gif) ,
,
于是.files/image488.gif) 为二面角
为二面角.files/image490.gif) 的平面角。…………………………8分
的平面角。…………………………8分
∵.files/image260.gif) ,
,.files/image262.gif) ,∴
,∴.files/image494.gif) ,
,.files/image496.gif)
在正方形.files/image256.gif) 中,作
中,作.files/image499.gif) 于
于.files/image501.gif) ,则
,则
.files/image503.gif) ,
,
∴.files/image505.gif) ,∴
,∴.files/image507.gif) 。
。
故二面角.files/image490.gif) 的大小为
的大小为.files/image510.gif) …………………………12分
…………………………12分
.files/image512.jpg) |
解法二:如图,以.files/image264.gif) 为原点,建立空间直角坐标系,使
为原点,建立空间直角坐标系,使.files/image515.gif) 轴,
轴,.files/image002.gif) 、
、.files/image518.gif) 分别在
分别在.files/image066.gif) 轴、
轴、.files/image521.gif) 轴上。
轴上。
(Ⅰ)由已知,.files/image523.gif) ,
,.files/image525.gif) ,
,.files/image527.gif) ,
,.files/image529.gif) ,
,.files/image531.gif) ,
,.files/image533.gif) ,
,
∴.files/image535.gif) ,
,
.files/image537.gif) ,
,.files/image539.gif) ,
,
∵.files/image541.gif) ,
∴
,
∴.files/image543.gif) ,
,
又.files/image545.gif) ,∴
,∴.files/image272.gif) ………………………………………4分
………………………………………4分
(Ⅱ)设.files/image548.gif) 为面
为面.files/image550.gif) 的法向量,则
的法向量,则.files/image552.gif) ,且
,且.files/image554.gif) 。
。
∵.files/image556.gif) ,
,.files/image535.gif) ,
,.files/image559.gif)
∴.files/image561.gif) ,取
,取.files/image563.gif) ,
,.files/image565.gif) ,
,.files/image567.gif) ,则
,则.files/image569.gif) ……………8分
……………8分
又.files/image571.gif) 为面
为面.files/image573.gif) 的法向量,所以
的法向量,所以.files/image575.gif) ,
,
因为二面角.files/image490.gif) 为锐角,所以其大小为
为锐角,所以其大小为.files/image578.gif) …………………………12分
…………………………12分
(20)解:
(Ⅰ).files/image580.gif) ……………………………………………………1分
……………………………………………………1分
(1)当.files/image582.gif) 时,由
时,由.files/image584.gif) ,知
,知.files/image586.gif) ,
,.files/image108.gif) 在
在.files/image589.gif) 单调递增
单调递增
而.files/image591.gif) ,则
,则.files/image282.gif) 不恒成立…………………………3分
不恒成立…………………………3分
(2)当.files/image594.gif) 时,令
时,令.files/image596.gif) ,得
,得.files/image598.gif)
当.files/image600.gif) 时,
时,.files/image602.gif) ,
,.files/image108.gif) 单调递增;
单调递增;.files/image605.gif) 时,
时,
.files/image607.gif) ,
,.files/image108.gif) 单调递减,
单调递减,.files/image108.gif) 在
在.files/image598.gif) 处取得极大值。
处取得极大值。
由于.files/image612.gif) ,所以
,所以.files/image614.gif) ,解得
,解得.files/image563.gif) ,即当且仅当
,即当且仅当.files/image563.gif) 时
时.files/image282.gif) 恒成立。
恒成立。
综上,所求.files/image284.gif) 的值为
的值为.files/image343.gif) …………………………7分
…………………………7分
(Ⅱ).files/image286.gif) 等价于
等价于.files/image621.gif) ,
,
下证这个不等式成立。
由(Ⅰ)知.files/image623.gif) ,即
,即.files/image625.gif) ,
,.files/image627.gif) ……………9分
……………9分
∴.files/image629.gif)
.files/image631.gif) …………………………12分
…………………………12分
(21)解:
(Ⅰ)曲线.files/image292.gif) 方程可写为
方程可写为.files/image634.gif) ,
,.files/image636.gif)
设.files/image638.gif) ,则
,则.files/image640.gif) ,又设
,又设.files/image642.gif) 、
、.files/image644.gif) 、
、.files/image646.gif)
曲线.files/image292.gif) 在点
在点.files/image018.gif) 处的切线斜率
处的切线斜率.files/image649.gif) ,则切线
,则切线.files/image268.gif) 方程为
方程为.files/image652.gif) ,
,
即.files/image654.gif) ,亦即
,亦即.files/image656.gif) …………………………3分
…………………………3分
分别将.files/image002.gif) 、
、.files/image004.gif) 坐标代入切线方程得
坐标代入切线方程得.files/image660.gif) ,
,.files/image662.gif)
∴.files/image664.gif) ,
,.files/image666.gif)
由.files/image308.gif) ,得
,得
.files/image669.gif) , ①
, ①
.files/image671.gif) , ②
, ②
∴.files/image673.gif) ……………7分
……………7分
∵.files/image675.gif) ,∴
,∴.files/image677.gif) ,
,
则由②式得.files/image679.gif) 。
。
从而曲线.files/image306.gif) 的方程为
的方程为.files/image682.gif)
.files/image684.gif) …………………………8分
…………………………8分
(Ⅱ).files/image066.gif) 轴与曲线
轴与曲线.files/image292.gif) 、
、.files/image306.gif) 交点分别为
交点分别为.files/image689.gif) 、
、.files/image691.gif) ,此时
,此时.files/image693.gif) ……9分
……9分
当.files/image208.gif) 、
、.files/image240.gif) 不在
不在.files/image066.gif) 轴上时,设直线
轴上时,设直线.files/image698.gif) 方程为
方程为.files/image700.gif) 。
。
若.files/image702.gif) ,则
,则.files/image208.gif) 、
、.files/image240.gif) 在第一象限,
在第一象限,
由.files/image706.gif) ,得
,得.files/image708.gif) ,由
,由.files/image710.gif) 得
得.files/image712.gif) ,
,
∴.files/image693.gif) ………………………………………11分
………………………………………11分
因为曲线.files/image292.gif) 和
和.files/image306.gif) 都关于
都关于.files/image066.gif) 轴对称,所以当
轴对称,所以当.files/image718.gif) 时,仍有
时,仍有.files/image693.gif)
综上,题设的.files/image318.gif) 为定值
为定值.files/image722.gif) …………………………12分
…………………………12分
(22)解:
(Ⅰ)由.files/image724.gif) ,且
,且.files/image327.gif) ,得
,得
当.files/image727.gif) 时,
时,
.files/image729.gif) ,解得
,解得.files/image731.gif) ;
;
当.files/image733.gif) 时,
时,.files/image735.gif) ,解得
,解得.files/image737.gif)
猜想:.files/image739.gif) ……………………………………………………2分
……………………………………………………2分
用数学归纳法证明如下
(1) 当.files/image727.gif) 时,命题显然成立。………………………………………3分
时,命题显然成立。………………………………………3分
(2) 假设当.files/image742.gif) 时命题成立,即
时命题成立,即.files/image744.gif) ,那么
,那么
由.files/image746.gif) ,得
,得
.files/image748.gif)
.files/image750.gif) 于是,当
于是,当.files/image752.gif) 时命题仍然成立………………………………………6分
时命题仍然成立………………………………………6分
根据(1)和(2),对任何.files/image288.gif) ,都有
,都有.files/image739.gif) …………………………7分
…………………………7分
(Ⅱ)当.files/image756.gif) 时,
时,.files/image758.gif) ,且对于
,且对于.files/image727.gif) 也成立。
也成立。
因此,.files/image761.gif)
对于.files/image627.gif) ,由
,由.files/image764.gif) ,得
,得
.files/image766.gif) ,……………10分
,……………10分
.files/image768.gif) ,
,
综上,.files/image770.gif) ………………………………………12分
………………………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com