（本题16分）

如图，F是抛物线的焦点，Q是准线与轴的交点，斜率为的直线经过点Q.

（1）当K取不同数值时，求直线与抛物线交点的个数；

（2）如直线与抛物线相交于A、B两点，求证：是定值

（3）在轴上是否存在这样的定点M，对任意的过点Q的直线，如与抛物线相交于A、B两点，均能使得为定值，有则找出满足条

件的点M；没有，则说明理由．

（满分16分）

某医药研究所开发一种新药，据检测，如果成人按规定的剂量服用，服药后每毫升血液中的含药量为（微克）与服药后的时间（小时）之间近似满足如图所示的曲线，其中OA 是线段，曲线 ABC 是函数（）的图象，且是常数．

（1）写出服药后y与x的函数关系式；

（2）据测定：每毫升血液中含药量不少于2 微克时治疗疾病有效．若某病人第一次服药时间为早上 6 : 00 ，为了保持疗效，第二次服药最迟应该在当天的几点钟？

（3）若按（2）中的最迟时间服用第二次药，则第二次服药3个小时后，该病人每毫升血液中含药量为多少微克。（结果用根号表示）

（本题16分）

如图，F是抛物线的焦点，Q是准线与轴的交点，斜率为的直线经过点Q.

（1）当K取不同数值时，求直线与抛物线交点的个数；

（2）如直线与抛物线相交于A、B两点，求证：是定值

（3）在轴上是否存在这样的定点M，对任意的过点Q的直线，如与抛物线相交于A、B两点，均能使得为定值，有则找出满足条

件的点M；没有，则说明理由．

（满分16分）
某医药研究所开发一种新药，据检测，如果成人按规定的剂量服用，服药后每毫升血液中的含药量为（微克）与服药后的时间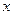（小时）之间近似满足如图所示的曲线，其中OA 是线段，曲线 ABC 是函数（）的图象，且是常数．

（1）写出服药后y与x的函数关系式；
（2）据测定：每毫升血液中含药量不少于2 微克时治疗疾病有效．若某病人第一次服药时间为早上 6 : 00 ，为了保持疗效，第二次服药最迟应该在当天的几点钟？
（3）若按（2）中的最迟时间服用第二次药，则第二次服药3个小时后，该病人每毫升血液中含药量为多少微克。（结果用根号表示）

本题满分16分）

如图，抛物线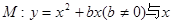轴交于O，A两点，交直线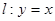于O，B两点，经过三点O，A，B作圆C。

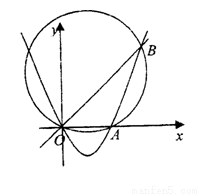
   （I）求证：当b变化时，圆C的圆心在一条定直线上；

   （II）求证：圆C经过除原点外的一个定点；

   （III）是否存在这样的抛物线M，使它的顶点与C的距离不大于圆C的半径？