
题目列表(包括答案和解析)
把函数 的图象按向量
的图象按向量 平移得到函数
平移得到函数 的图象.
的图象.
(1)求函数 的解析式; (2)若
的解析式; (2)若 ,证明:
,证明: .
.
【解析】本试题主要考查了函数 平抑变换和运用函数思想证明不等式。第一问中,利用设 上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入
上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入 ,便可以得到结论。第二问中,令
,便可以得到结论。第二问中,令 ,然后求导,利用最小值大于零得到。
,然后求导,利用最小值大于零得到。
(1)解:设 上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入
上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入 得y-2=ln(x+1)-2即y=ln(x+1),所以
得y-2=ln(x+1)-2即y=ln(x+1),所以 .……4分
.……4分
(2) 证明:令 ,……6分
,……6分
则 ……8分
……8分
 ,∴
,∴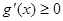 ,∴
,∴ 在
在 上单调递增.……10分
上单调递增.……10分
故 ,即
,即
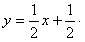
| A+B |
| 2 |
| A-B |
| 2 |
| A+B |
| 2 |
| A-B |
| 2 |
| A+B |
| 2 |
| A-B |
| 2 |
阅读下面材料:根据两角和与差的正弦公式,有
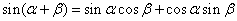 ----------①
----------①
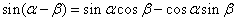 ------②
------②
由①+② 得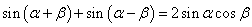 ------③
------③
令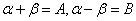 有
有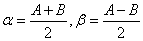
代入③得
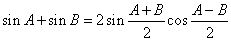 .
.
(1)利用上述结论,试求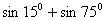 的值。
的值。
(2)类比上述推证方法,根据两角和与差的余弦公式,证明: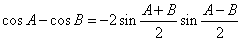 ;
;
对于解方程x2-2x-3=0的下列步骤:
①设f(x)=x2-2x-3
②计算方程的判别式Δ=22+4×3=16>0
③作f(x)的图象
④将a=1,b=-2,c=-3代入求根公式
x=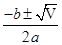 ,得x1=3,x2=-1.
,得x1=3,x2=-1.
其中可作为解方程的算法的有效步骤为( )
A.①② B.②③
C.②④ D.③④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com