
题目列表(包括答案和解析)
(本小题满分12分)
已知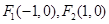 ,点
,点 满足
满足 ,记点
,记点 的轨迹为
的轨迹为 .
.
(Ⅰ)求轨迹 的方程;
的方程;
(Ⅱ)过点F2(1,0)作直线l与轨迹 交于不同的两点A、B,设
交于不同的两点A、B,设 ,若
,若 的取值范围
的取值范围
在圆
 上任取一点
上任取一点 ,过点
,过点 作
作 轴的垂线段
轴的垂线段 ,
, 为垂足.当点
为垂足.当点 在圆上运动时,线段
在圆上运动时,线段 的中点
的中点 形成轨迹
形成轨迹 .
.
(1)求轨迹 的方程;
的方程;
(2)若直线 与曲线
与曲线 交于
交于 两点,
两点, 为曲线
为曲线 上一动点,求
上一动点,求 面积的最大值
面积的最大值
经过点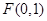 且与直线
且与直线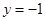 相切的动圆的圆心轨迹为
相切的动圆的圆心轨迹为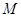 .点
.点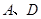 在轨迹
在轨迹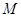 上,且关于
上,且关于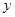 轴对称,过线段
轴对称,过线段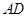 (两端点除外)上的任意一点作直线
(两端点除外)上的任意一点作直线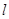 ,使直线
,使直线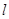 与轨迹
与轨迹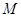 在点
在点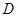 处的切线平行,设直线
处的切线平行,设直线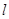 与轨迹
与轨迹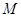 交于点
交于点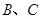 .
.
(1)求轨迹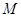 的方程;
的方程;
(2)证明: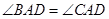 ;
;
(3)若点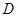 到直线
到直线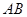 的距离等于
的距离等于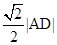 ,且
,且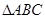 的面积为20,求直线
的面积为20,求直线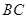 的方程.
的方程.
在直角坐标系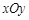 中,点
中,点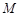 到点
到点 ,
,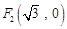 的距离之和是
的距离之和是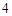 ,点
,点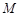 的轨迹
的轨迹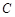 与
与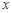 轴的负半轴交于点
轴的负半轴交于点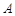 ,不过点
,不过点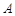 的直线
的直线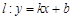 与轨迹
与轨迹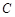 交于不同的两点
交于不同的两点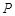 和
和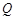 .
.
⑴求轨迹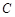 的方程;
的方程;
⑵当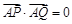 时,证明直线
时,证明直线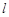 过定点.
过定点.
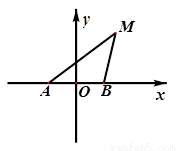
(本小题满分12分) 如图,动点 与两定点
与两定点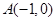 、
、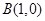 构成
构成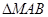 ,且直线
,且直线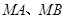 的斜率之积为4,设动点
的斜率之积为4,设动点 的轨迹为
的轨迹为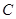 。
。
(Ⅰ)求轨迹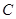 的方程;
的方程;
(Ⅱ)设直线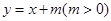 与
与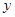 轴交于点
轴交于点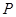 ,与轨迹
,与轨迹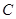 相交于点
相交于点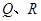 ,且
,且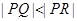 ,求
,求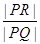 的取值范围。
的取值范围。
1、A 2,、B 3、 D 4,、B 5、 D 6、C 7、A 8、B 9、A 10、D
11、(,1] 12、-或1 13、6p 14、2 15、11
16解:解:(Ⅰ)



当 ,即
,即
 时,
时, 取得最大值
取得最大值 .
.
(Ⅱ)当 ,即
,即
 时,
时,
所以函数 的单调递增区间是
的单调递增区间是

17、解:(Ⅰ)从15名教师中随机选出2名共 种选法, …………………………2分
种选法, …………………………2分
所以这2人恰好是教不同版本的男教师的概率是 . …………………5分
. …………………5分
(Ⅱ)由题意得
 ;
;  ;
; .
.
故 的分布列为
的分布列为

0
1
2





所以,数学期望 .
.
18、解法一:(Ⅰ)证明:连接





 ∥
∥ 。 ……………………3分
。 ……………………3分

 ∥平面
∥平面 …………………………5分
…………………………5分
(Ⅱ)解:在平面



 ―
― ―
― ……………………8分
……………………8分
设 。
。
在
所以,二面角 ―
― ―
― 的大小为
的大小为 。 ………………12分
。 ………………12分
19、(I)解:当
①当 , 方程化为
, 方程化为

②当 , 方程化为1+2x
= 0, 解得
, 方程化为1+2x
= 0, 解得 ,
,
由①②得, 
(II)解:不妨设 ,
,
因为
所以 是单调递函数, 故
是单调递函数, 故 上至多一个解,
上至多一个解,

20、解:(Ⅰ)由
 知,点
知,点 的轨迹
的轨迹 是以
是以 、
、 为焦点的双曲线右支,由
为焦点的双曲线右支,由 ,∴
,∴ ,故轨迹E的方程为
,故轨迹E的方程为 …(3分)
…(3分)
(Ⅱ)当直线l的斜率存在时,设直线l方程为 ,与双曲线方程联立消
,与双曲线方程联立消 得
得 ,设
,设 、
、 ,
,
|