(1)求a的值;

　　(2)求函数f(x)＋g(x)的单调递增区间；

　　(3)若n为正整数,证明：10^f(n)·()^g(n)<4.

已知函数f(x)＝为偶函数，且函数y＝f(x)图象的两相邻对称轴间的距离为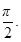

　　(1)求f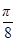（）的值；

　　(2)将函数y＝f(x)的图象向右平移个单位后，再将得到的图象上各点的横坐标伸长到原来的4倍，纵坐标不变，得到函数y＝g(x)的图象，求g(x)的单调递减区间.

(12分)已知：函数，                                                            

　　(1)求：函数f(x)的定义域；

　　(2)判断函数f(x)的奇偶性并说明理由；

　　(3)判断函数f(x)在()上的单调性，并用定义加以证明。

（08年新建二中模拟文） (12分)    已知是定义在R上的函数，其图象交x轴于A、B、C三点．若点B的坐标为 (2，0)，且f (x) 在[－1，0]和[4，5]上有相同的单调性，在[0，2]和[4，5]上有相反的单调性．
　　(1)求c的值；
　　(2)在函数f (x)的图象上是否存在一点M(x₀，y₀)，使得f (x)在点M的切线斜率为3b？若存在，求出点M的坐标；若不存在，请说明理由；
　　(3)求| AC |的取值范围．