（10分） 体育课进行篮球投篮达标测试。规定：每位同学有5次投篮机会，若

投中3次则“达标”；为节省时间，同时规定：若投篮不到5次已达标，则停止投篮；若即

便后面投篮全中，也不能达标（前3次投中0次）则也停止投篮。同学甲投篮命中率是，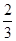

且每次投篮互不影响。

（1）求同学甲测试达标的概率；

（2）设测试同学甲投篮次数记为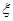，求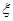的分布列及数学期望。

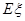A.①是真命题，②是假命题

B.①是假命题，②是真命题

C.①②都是真命题

D.①②都是假命题

已知函数．（）

（1）若在区间上单调递增，求实数的取值范围；

（2）若在区间上，函数的图象恒在曲线下方，求的取值范围．

【解析】第一问中，首先利用在区间上单调递增，则在区间上恒成立，然后分离参数法得到，进而得到范围；第二问中，在区间上，函数的图象恒在曲线下方等价于在区间上恒成立．然后求解得到。

解：（1）在区间上单调递增，

则在区间上恒成立．  …………3分

即，而当时，，故． …………5分

所以．                 …………6分

（2）令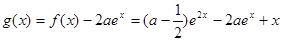，定义域为．

在区间上，函数的图象恒在曲线下方等价于在区间上恒成立．   

∵        …………9分

① 若，令，得极值点，，

当，即时，在（，+∞)上有，此时在区间上是增函数，并且在该区间上有，不合题意；

当，即时，同理可知，在区间上递增，

有，也不合题意；                     …………11分

② 若，则有，此时在区间上恒有，从而在区间上是减函数；

要使在此区间上恒成立，只须满足，

由此求得的范围是．        …………13分

综合①②可知，当时，函数的图象恒在直线下方．

已知S_n是数列{a_n}的前n项和，（n≥2，n∈N^*），且．
（1）求a₂的值，并写出a_n和a_n+1的关系式；
（2）求数列{a_n}的通项公式及S_n的表达式；
（3）我们可以证明：若数列{b_n}有上界（即存在常数A，使得b_n＜A对一切n∈N^*恒成立）且单调递增；或数列{b_n}有下界（即存在常数B，使得b_n＞B对一切n∈N^*恒成立）且单调递减，则存在．直接利用上述结论，证明：存在．