题目列表(包括答案和解析)
（2009?潍坊模拟）如图甲所示，平行金属导轨竖直放置，导轨间距为L=1m，上端接有电阻R1=3Ω，下端接有电阻R2=6Ω，虚线OO′下方是垂直于导轨平面的匀强磁场．现将质量m=0.1kg、电阻不计的金属杆ab，从OO′上方某处垂直导轨由静止释放，杆下落0.2m过程中始终与导轨保持良好接触，加速度a与下落距离h的关系图象如图乙所示．求：
（2009?天津模拟）如图甲所示，abcd是位于竖直平面内的正方形闭合金属线框，底边bc水平，金属线框的质量为m，电阻为R．在金属线框的下方有一水平方向的匀强磁场区域，MN和M′N′是匀强磁场区域的上下边界，并与线框的bc边平行，磁场方向与线框平面垂直．现金属线框从磁场上方某一高度处由静止开始下落，图乙是金属线框由开始下落到完全穿过磁场区域瞬间的速度-时间图象，图象中坐标轴上所标出的字母均为已知量，重力加速度为g，忽略空气阻力．求：
（2009?天津模拟）甲、乙两辆汽车沿同一平直路面行驶，它们由同一位置出发后的v-t图象如图所示，下列说法正确的是（ ）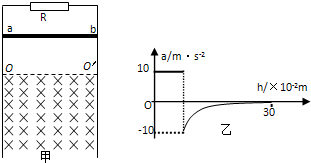
（2011?徐州一模）如图甲所示，两条足够长的光滑平行金属导轨竖直放置，导轨问距为L=1m，两导轨的，上端间接有电阻，阻值R=2Ω 虚线OO′下方是垂宣予导轨平面向里的匀强磁场，磁场磁感应强度为2T，现将质量m=0.1kg电阻不计的金届杆ab，从OO′上方某处由静止释放，金属杆在下落的过程中与导轨保持良好接触，且始终保持水平，不计导轨的电阻．已知金属杆下落0.3m的过程中加速度a与下落距离h的关系图象如图乙所示．求：
（2009?上海模拟）在如图甲所示的电路中，电源电动势为3.0V，内阻不计，L1、L2、L3为3个相同规格的小灯泡，这种小灯泡的伏安特性曲线如图乙所示，当开关S闭合后（ ）1.ABD 2.BD 3.D 4.BD 5.AC 6.B 7.BC 8.D 9.AB 10.D 11.D 12.AD
13. 碳粒 （2分） 液体分子运动的无规则性 （3分）
系统或气体（1分） 外界（1分） 下降 （3分）
14.(每空2分) 沿Ｙ轴负方向； 5； 32
红色明暗相间的条纹；没有干涉条纹，仍有亮光。
15．（14分）
（1）（4分）10.501（10.500-10.502） 10.155
（2）（一）①将长木板一端垫起，让小车重力
沿斜面的分力平衡摩擦阻力；（1分）
②小车质量远大于沙桶的总质量。（1分）
（二）0.86，（1分）
，（2分）
0.64（1分）
(三) ①如图（无标度、图线作成折线或曲线
均不能得分）（2分） ② AB（2分）
16．（10分）
（1）C（2分） （2）（图略）（2分）
（3）方法一 a．
（2分）
b．如（方法一）图（2分）
c．纵轴截距的倒数（1分） 斜率除以纵轴的截距（1分）
方法二 a．
（2分）
b．如（方法二）图（2分）
c．斜率除以纵轴截距的绝对值（1分） 纵轴截距的倒数的绝对值（1分）
17.(1)解：从起跳到最高点的时间t1,
由H=
gt
得
（2分）
t1=
=
s=0.3s
（1分）
从最高点到手触水面过程的时间为t
h+H=
gt
得
（2分）
t=
=
s≈1.4s （1分）
所以t1+ t=1.7s
（2分）
(2)飞镖作平抛运动，飞镖飞行时间为
t=
=0.1s
（2分）
飞镖在竖直方向的位移h
由h=gt=0.05m
（2分）
当考虑空气水平阻力时，飞镖水平方向做匀减速运动
a=
=
设第二次投掷飞镖速度为v/
由s=v/
t?a t2得
（2分）
v/=
18.解：
设小物体滑到B时速度为V
，滑槽速度为V，由系统水平方向动量守恒及系统机械能守恒得：
mV=MV
（2分）
mg(H+R)=mV
+MV
（2分）
解得：V=4m/s （2分）
V=
之后小物体进入水平表面，而滑槽由于撞墙，速度变为0，设两者同速为V，相对位移为S，由系统动量守恒及功能关系，得
mV=(m+M)V
（2分）
μmgS=mV?(m+M)V
（2分）
解得S=
所以最终小物体离C端x=（3-1.6）m=1.4m （2分）
19.解：
(1)设线圈ab边刚好进入磁场时，速度为v1，加速度为a, 对两个物体组成的系统，根据机械能守恒得： 
① （2分）
ab边上的感应电动势为：
②
（1分）
线圈中的感应电流为：
③
（1分）
ab边所受的安培力为：
④
（1分）
设绳上的拉力为T，选加速度作为正方向，对重物与线圈分别利用牛顿第二定律可得：
⑤
（1分）
⑥
（2分）
联立以上几式可得：
（2分）
(2)设线圈的cd边刚好进入磁场时速度为v2，由于线圈向上运动进出磁场的两个边界过程的运动情况完全一样，故线圈ab边到达磁场上边界时的速度必定是v1，线圈cd边刚好出磁场时速度为v2。整个线圈在磁场中时，由机械能守恒有：
⑦ （2分）
对整个过程中，由能量守恒有：
⑧ （2分）
故焦耳热为：
⑨ （2分）
20.解：（1）带电粒子穿过磁场时，速度变为水平，由左手定则知，带电粒子带负电；（1分）
粒子射入电场后从下板边缘飞出，粒子所受电场力向下，故上板带负电。（1分）
（2）设粒子的速度为v0,粒子在电场中作类平抛运动，飞越两金属板间需时间T
水平方向有：
① （1分）
竖直方向有：
② （1分）
解得：
，
。（1分）
设粒子在磁场中做圆周运动的半径为R，
由牛顿第二定律有：
③ （2分）
设磁场的最小半径为r，由几何关系得：
④ （1分）
故磁场的最小面积为：
⑤ （2分）
（3）粒子飞越电场的时间为一定值T，粒子运动的加速度为：
⑥ （1分）
若粒子从t=0、2×10-5s、4×10-5s ……时刻进入，在时间T内侧向移动距离为：
⑦
（1分）
设粒子恰好从下板右边缘水平飞出，则有：
⑧
（1分）
解得：
设粒子进入板间向下加速时间为
，据对称性可知再历时粒子竖直速度为零，
对以上过程，粒子向下的位移为：
⑨
（1分）
要使粒子不碰板而飞出，应满足： 
⑩ （2分）
联立⑧⑨解得：
故粒子能飞出两板间对应的入射时刻为：
（k=0，1，2，……） （2分）
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com