
∴SO⊥平面ABC。
如图建系为O―xyz。
则A(2,0,0),B(0,2 )
)
C(―2,0,0),S(0,0, ),
),
M(1, ),N(
),N( ),
),

则
∴AC⊥SB.……………………6分
(2)由(1)得
设

 为平面ABC的法向量,
为平面ABC的法向量,
∴
∴二面角N-CM-B的大小为 ……………………………………………14分
……………………………………………14分
17.(本小题满分13分)
解:(Ⅰ)由题意C,A1,A2,A3四点构成一个正三棱锥,CA1,CA2,CA3为该三棱锥
的三条侧棱,………………………………………………………………2分
三棱锥的侧棱 ……………………………………4分
……………………………………4分
于是有 (0<x<2)……………………………5分
(0<x<2)……………………………5分
(Ⅱ)对y求导得 ……………………………………8分
……………………………………8分
令 =0得
=0得 解得
解得 或
或 (舍),……10分
(舍),……10分
当
故当 时,即BC=1.5m时,y取得最小值为6m。………………………13分
时,即BC=1.5m时,y取得最小值为6m。………………………13分
18.(本小题满分13分)
解:(Ⅰ)记“恰好射击5次引爆油罐”的事件为事件A,
则 ……………………………………4分
……………………………………4分
(Ⅱ)射击次数 的可能取值为2,3,4,5。…………………………………5分
的可能取值为2,3,4,5。…………………………………5分
 =
= ;
;
 =
= ;
;
 =
= ;
;
 =
= 。……………………………………11分
。……………………………………11分
故 的分布列为
的分布列为

2
3
4
5
P




……………………………………………………………………………12分
E =2×
=2× +3×
+3× +4×
+4× +5×
+5× =
=
故所求的数学期望为 ………………………………………………13分
………………………………………………13分
19.(本小题满分13分)
解:(Ⅰ)由于四边形OFPM是菱形,故
作双曲线的右准线交PM于点H。
则 …………………………………………………3分
…………………………………………………3分
所以离心率

整理得 解得
解得 或
或 (舍)。
(舍)。
故所求双曲线的离心率为2。……………………………………………5分

(Ⅱ)由 得 得 ,又 ,又 故 故 。 。 双曲线方程为 。 。 设P的横坐标为 ,由 ,由 得 得 即 即 = = a a 将其带入双曲线方程 解得 即 即 7分 7分  ,故直线AB的方程为 ,故直线AB的方程为 8分 8分 将直线AB方程代入双曲线方程 10分 10分 由 得 得 解得 ,则 ,则 所求双曲线方程为 13分 13分 20.(本小题满分14分) 解:(1)当 时, 时, ,所以 ,所以 两边取倒数,得 ,即 ,即 =-1,又 =-1,又 所以数列 是首项为―1,公差d= ―1的等差数列………………3分 是首项为―1,公差d= ―1的等差数列………………3分 故 , , 所以 即数列 的通项公式为 的通项公式为 ……………………4分 ……………………4分 (2)根据题意,只需当 时,方程 时,方程 有解,………………5分 有解,………………5分 即方程 有不等式a的解 有不等式a的解 将x=a代入方程左边,左边为1,与右边不相等。 故方程不可能有解x=a。……………………7分 由 ,得 ,得 . . 即实数a的取值范围是 ……………………10分 ……………………10分 (3)假设存在实数a,使处取定义域中的任一实数值作为x1,都可以用上述方法构造出一个无穷数列{ }, }, 那么根据题意可知, 中无解,……………………12分 中无解,……………………12分 即当 无实数解. 无实数解. 由于 的解。 的解。 所以对任意 无实数解, 无实数解, 因此 , , 故a= ―1即为所求a的值…………………………14分
| |

 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.请在答题纸指定区域内 作答.解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.请在答题纸指定区域内 作答.解答应写出文字说明、证明过程或演算步骤. 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.请在答题纸指定区域内 作答.解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.请在答题纸指定区域内 作答.解答应写出文字说明、证明过程或演算步骤.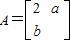 属于特征值-1的一个特征向量为
属于特征值-1的一个特征向量为 ,求矩阵A的逆矩阵.
,求矩阵A的逆矩阵. (t为参数,t∈{R}).试求曲线C上点M到直线l的距离的最大值.
(t为参数,t∈{R}).试求曲线C上点M到直线l的距离的最大值.




 10.
10. 11.
11. 12.
12. 13.50 14.5
13.50 14.5 ………………2分
………………2分
 ……………………3分
……………………3分 ……………………5分
……………………5分 ,
, …………………………6分
…………………………6分 ,所以
,所以
 …………………………7分
…………………………7分
 ,
, .
. .……………………11分
.……………………11分 ……………………12分
……………………12分
 ……………………13分
……………………13分 DE⊥CM,BM⊥CM,
DE⊥CM,BM⊥CM,