练习册

  • 练习册
  • 试题
    方法二:设点到平面的距离为. 【查看更多】

     

    题目列表(包括答案和解析)

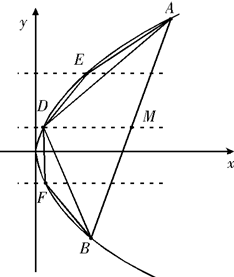    （2007•浦东新区二模）已知抛物线C：y2=2px（p＞0）上横坐标为4的点到焦点的距离为5．
    （1）求抛物线C的方程．
    （2）设直线y=kx+b（k≠0）与抛物线C交于两点A（x1，y1），B（x2，y2），且|y1-y2|=a（a＞0），M是弦AB的中点，过M作平行于x轴的直线交抛物线C于点D，得到△ABD；再分别过弦AD、BD的中点作平行于x轴的直线依次交抛物线C于点E，F，得到△ADE和△BDF；按此方法继续下去．
    解决下列问题：
    ①求证：a2=
    16(1-kb)k2
    ；
    ②计算△ABD的面积S△ABD；
    ③根据△ABD的面积S△ABD的计算结果，写出△ADE，△BDF的面积；请设计一种求抛物线C与线段AB所围成封闭图形面积的方法，并求出此封闭图形的面积．

    查看答案和解析>>

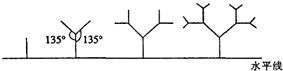
    一种树形图形为：第一层是一条与水平线垂直的线段，长度为1；第二层在第一层线段的前端作两条与线段成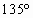角的线段，长度为其一半；第三层按第二层的方法在第一线段的前端生成两条线段，重复前面的作法作图到第n层，设树的第n层最高点至水平线的距离为到第n层的树形的总高度．试求：

    (1)到第三层及第四层的树形图的总高度；

    (2)到第n层的树形图的总高度hn；

    (3)若树形的高度大于2，则称树形图为“高大”，否则“矮小”，试作判断该树形是“高大”还是“矮小”呢？

    查看答案和解析>>

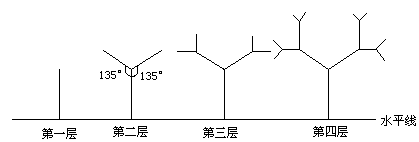
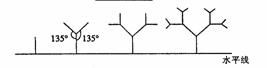
    如图所示，一种树形图为：第一层是一条与水平线垂直的线段，长度为1；第二层在第一层线段的前端作两条与其成角的线段，长度为其一半；第三层按第二层的方法在每一条线段的前端生成两条线段，重复前面的作法作图至第层，设树形的第层的最高点至水平线的距离为第层的树形的总高度，则到第四层的树形图的总高度      ，当为偶数时，到第层的树形图的总高度       。

    查看答案和解析>>

    如图所示，一种树形图为：第一层是一条与水平线垂直的线段，长度为第二层在第一层线段的前端作两条与其成135°角的线段，长度为其一半；第三层按第二层的方法在每一条线段的前端生成两条线段．重复前面的作法作图至第《层，设树形的第n层的最高点至水平线的距离为第W层的树形的总高度，则到第四层的树形图的总高度h4=
    5
    4
    +
    5
    		2
    16
    5
    4
    +
    5
    		2
    16
    ，当n为偶数时，到第《层的树形图的总高度hn=
    4+
    		2
    3
    [1-(
    1
    2
    )    n    ]
    4+
    		2
    3
    [1-(
    1
    2
    )    n    ]

    查看答案和解析>>

    如图所示，一种树形图为：第一层是一条与水平线垂直的线段，长度为第二层在第一层线段的前端作两条与其成135°角的线段，长度为其一半；第三层按第二层的方法在每一条线段的前端生成两条线段．重复前面的作法作图至第《层，设树形的第n层的最高点至水平线的距离为第W层的树形的总高度，则到第四层的树形图的总高度h4=________，当n为偶数时，到第《层的树形图的总高度hn=________

    查看答案和解析>>


    同步练习册答案