
题目列表(包括答案和解析)
设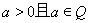 ,
,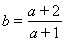 .
.
(Ⅰ)证明: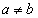 ;
;
(Ⅱ)求证:在数轴上,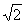 介于
介于 与
与 之间,且距
之间,且距 较远;
较远;
(Ⅲ)在数轴上, 之间的距离是否可能为整数?若有,则求出这个整数;若没有,
之间的距离是否可能为整数?若有,则求出这个整数;若没有,
说明理由.
设 ,
, .
.
(Ⅰ)证明: ;
;
(Ⅱ)求证:在数轴上,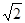 介于
介于 与
与 之间,且距
之间,且距 较远;
较远;
(Ⅲ)在数轴上,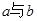 之间的距离是否可能为整数?若有,则求出这个整数;若没有,
之间的距离是否可能为整数?若有,则求出这个整数;若没有,
说明理由.
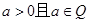 ,
, .
. ;
;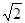 介于
介于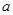 与
与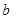 之间,且距
之间,且距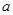 较远;
较远;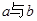 之间的距离是否可能为整数?若有,则求出这个整数;若没有,
之间的距离是否可能为整数?若有,则求出这个整数;若没有,17.证明:假设f(x)至少有两个零点。不妨设有两个零点![]() 与
与![]() ,则f(
,则f(![]() )=0,f(
)=0,f(![]() )=0
)=0
所以f(![]() )=f(
)=f(![]() )与已知f(x)是单调函数矛盾,所以假设错误,因此f(x)在其定义域上是单调函数证明f(x)至多有一个零点
)与已知f(x)是单调函数矛盾,所以假设错误,因此f(x)在其定义域上是单调函数证明f(x)至多有一个零点
一批产品共10件,其中7件正品,3件次品,每次从这批产品中任取一件,在下述三种情况下,分别求直至取得正品时所需次数X的概率分布。
(1)每次取出的产品不再放回去;
(2)每次取出的产品仍放回去;
(3)每次取出一件次品后,总是另取一件正品放回到这批产品中.
| x |
| x+1 |
| an+1 |
| an |
| ||
| 2 |
| 1 |
| an |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com