
题目列表(包括答案和解析)
设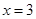 是函数
是函数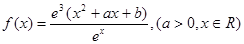 的一个极值点.
的一个极值点.
(1)求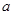 与
与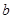 的关系式(用
的关系式(用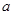 表示
表示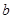 ),并求
),并求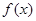 的单调递增区间;
的单调递增区间;
(2)设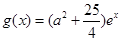 ,若存在
,若存在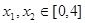 使得
使得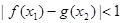 成立,求实数
成立,求实数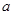 的取值范围.
的取值范围.
设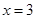 是函数
是函数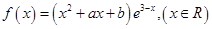 的一个极值点。
的一个极值点。
(1)求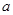 与
与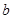 的关系式(用
的关系式(用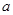 表示
表示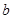 ),并求
),并求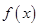 的单调区间;
的单调区间;
(2)设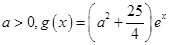 ,若存在
,若存在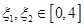 ,使得
,使得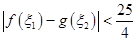 成立,求实数
成立,求实数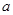 的取值范围。
的取值范围。
设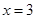 是函数
是函数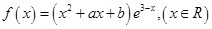 的一个极值点。
的一个极值点。
(1)求 与
与 的关系式(用
的关系式(用 表示
表示 ),并求
),并求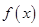 的单调区间;
的单调区间;
(2)设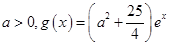 ,若存在
,若存在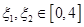 ,使得
,使得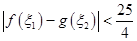 成立,求实数
成立,求实数 的取值范围。
的取值范围。
设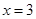 是函数
是函数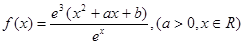 的一个极值点.
的一个极值点.
(1)求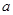 与
与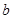 的关系式(用
的关系式(用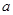 表示
表示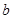 ),并求
),并求 的单调递增区间;
的单调递增区间;
(2)设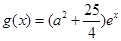 ,若存在
,若存在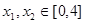 使得
使得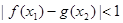 成立,求实数
成立,求实数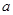 的取值范围.
的取值范围.
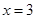 是函数
是函数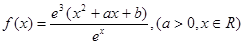 的一个极值点.
的一个极值点.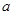 与
与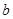 的关系式(用
的关系式(用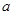 表示
表示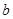 ),并求
),并求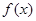 的单调递增区间;
的单调递增区间;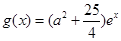 ,若存在
,若存在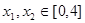 使得
使得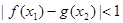 成立,求实数
成立,求实数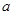 的取值范围.
的取值范围.一、填空题:
1.----数学.files/image286.gif) ;2. 79 ;3.1; 4.
;2. 79 ;3.1; 4. ----数学.files/image288.gif) ; 5.
; 5.----数学.files/image290.gif) ;6.
;6. ----数学.files/image292.gif) ; 7.16 ;8.7;
9.2;
10.
; 7.16 ;8.7;
9.2;
10. ----数学.files/image294.gif) ; 11.
; 11. ----数学.files/image296.gif) ; 12.
; 12. ----数学.files/image298.gif) ; 13. 2; 14. 3955.
; 13. 2; 14. 3955.
特别说明:有消息说,今年数学的填空题的压轴题将比较新、比较难,我们在评讲时要教育学生有这方面的心理准备。
二、解答题:
15.解:(1)----数学.files/image300.gif)
----数学.files/image302.gif)
∵----数学.files/image119.gif) ∴
∴----数学.files/image304.gif) ┉┉┉┉┉┉┉┉┉┉┉┉┉4分
┉┉┉┉┉┉┉┉┉┉┉┉┉4分
----数学.files/image306.gif)
----数学.files/image308.gif) ┉┉┉┉┉┉┉7分
┉┉┉┉┉┉┉7分
(2)∵(
由正弦定理得(2sinA-sinC)cosB=sinBcosC┉┉┉┉┉┉8分
∴2sinAcosB-sinCcosB=sinBcosC ∴2sinAcosB=sin(B+C)
∵----数学.files/image310.gif) ∴
∴----数学.files/image312.gif) ,
,
∴----数学.files/image314.gif) ┉┉┉┉┉┉10分
┉┉┉┉┉┉10分
∴----数学.files/image316.gif) ┉┉┉┉┉┉11分
┉┉┉┉┉┉11分
∴----数学.files/image318.gif) ┉┉┉┉┉┉12分
┉┉┉┉┉┉12分
又∵----数学.files/image320.gif) ,∴
,∴----数学.files/image322.gif) ┉┉┉┉┉┉13分
┉┉┉┉┉┉13分
故函数f(A)的取值范围是----数学.files/image324.gif) ┉┉┉┉┉┉14分
┉┉┉┉┉┉14分
16. 解:(1)∵函数----数学.files/image326.gif) 的图象的对称轴为
的图象的对称轴为----数学.files/image328.gif)
要使----数学.files/image326.gif) 在区间
在区间----数学.files/image331.gif) 上为增函数,
上为增函数,
当且仅当----数学.files/image129.gif) >0且
>0且----数学.files/image333.gif) ……………………………3分
……………………………3分
若----数学.files/image129.gif) =1则
=1则----数学.files/image131.gif) =-1,
=-1,
若----数学.files/image129.gif) =2则
=2则----数学.files/image131.gif) =-1,1
=-1,1
若----数学.files/image129.gif) =3则
=3则----数学.files/image131.gif) =-1,1;
……………………………5分
=-1,1;
……………………………5分
∴事件包含基本事件的个数是1+2+2=5
∴所求事件的概率为----数学.files/image335.gif) ……………………………7分
……………………………7分
(2)由(Ⅰ)知当且仅当----数学.files/image337.gif) 且
且----数学.files/image129.gif) >0时,
>0时,
函数----数学.files/image339.gif) 上为增函数,
上为增函数,
依条件可知试验的全部结果所构成的区域为----数学.files/image341.gif)
构成所求事件的区域为三角形部分。 ………………………………9分
由----数学.files/image343.gif) ……………………………11分
……………………………11分
∴所求事件的概率为----数学.files/image345.gif) …………………………… 14分
…………………………… 14分
17. (1)证明: ----数学.files/image347.gif) 平面
平面----数学.files/image349.gif) 平面
平面----数学.files/image351.gif) ,
,----数学.files/image353.gif) ,
,
平面----数学.files/image355.gif) 平面
平面----数学.files/image351.gif) =
=----数学.files/image358.gif) ,
,----数学.files/image360.gif) 平面
平面----数学.files/image351.gif) ,
,
----数学.files/image363.gif) 平面
平面----数学.files/image351.gif) ,
,----数学.files/image366.gif) ,……… 2分
,……… 2分
又----数学.files/image368.gif) 为圆
为圆----数学.files/image370.gif) 的直径,
的直径,----数学.files/image372.gif) ,
, ----数学.files/image374.gif) 平面
平面----数学.files/image376.gif) 。……… 5分
。……… 5分
(2)设----数学.files/image378.gif) 的中点为
的中点为----数学.files/image380.gif) ,则
,则----数学.files/image382.gif)
----数学.files/image384.gif)
----数学.files/image386.gif) ,又
,又----数学.files/image388.gif)
----数学.files/image384.gif)
----数学.files/image386.gif) ,则
,则----数学.files/image382.gif)
----数学.files/image384.gif)
----数学.files/image388.gif) ,
,----数学.files/image393.gif) 为平行四边形,
……… 7分
为平行四边形,
……… 7分
----数学.files/image395.gif)
----数学.files/image397.gif) ,又
,又----数学.files/image399.gif) 平面
平面----数学.files/image401.gif) ,
,----数学.files/image403.gif) 平面
平面----数学.files/image401.gif) ,
,
----数学.files/image395.gif) 平面
平面----数学.files/image401.gif) 。……… 9分
。……… 9分
(3)过点----数学.files/image406.gif) 作
作----数学.files/image408.gif) 于
于----数学.files/image255.gif) ,
,----数学.files/image347.gif) 平面
平面----数学.files/image349.gif) 平面
平面----数学.files/image351.gif) ,
,
----数学.files/image411.gif) 平面
平面----数学.files/image413.gif) ,
,----数学.files/image415.gif) ,……… 11分
,……… 11分
----数学.files/image417.gif) 平面
平面----数学.files/image351.gif) ,
,
----数学.files/image419.gif)
----数学.files/image421.gif) ,……… 14分
,……… 14分
----数学.files/image423.gif)
----数学.files/image425.gif) . ……… 15分
. ……… 15分
18. 解:(1)因为直线----数学.files/image192.gif) :
:----数学.files/image427.gif) 过定点T(4,3)……… 2分
过定点T(4,3)……… 2分
由题意,要使圆----数学.files/image370.gif) 的面积最小, 定点T(4,3)在圆上,
的面积最小, 定点T(4,3)在圆上,
所以圆----数学.files/image370.gif) 的方程为
的方程为----数学.files/image430.gif) ;……… 4分
;……… 4分
(2)A(-5,0),B(5,0),设----数学.files/image432.gif) ,则
,则----数学.files/image434.gif) ……(1)
……(1)
----数学.files/image436.gif) ,
,----数学.files/image438.gif) ,
,
由----数学.files/image440.gif) 成等比数列得,
成等比数列得,----数学.files/image442.gif) ,
,
即----数学.files/image444.gif) ,整理得:
,整理得:----数学.files/image446.gif) ,
,
即----数学.files/image448.gif) ……(2)
……(2)
由(1)(2)得:----数学.files/image450.gif) ,
,----数学.files/image452.gif) ,
,
----数学.files/image454.gif) ……………………… 9分
……………………… 9分
(3)----数学.files/image456.gif)
----数学.files/image458.gif) ,……… 11分
,……… 11分
由题意,得直线----数学.files/image192.gif) 与圆O的一个交点为M(4,3),又知定点Q(
与圆O的一个交点为M(4,3),又知定点Q(----数学.files/image208.gif) ,3),
,3),
直线----数学.files/image460.gif) :
:----数学.files/image462.gif) ,
,----数学.files/image464.gif) ,则当
,则当----数学.files/image466.gif) 时
时----数学.files/image468.gif) 有最大值32. ……… 14分
有最大值32. ……… 14分
即----数学.files/image470.gif) 有最大值为32,
有最大值为32,
此时直线----数学.files/image076.gif) 的方程为
的方程为----数学.files/image472.gif) .……… 15分
.……… 15分
特别说明:第19题、第20题不是完整的压轴题,原作者都有第3问设计,为了强化考试策略教育,让学生有信心做压轴题的开始一两问,并在考前体会做好基础题可以拿高分,我们特意进行了删减处理。特别优秀的班级(如市中的奥班,可以添加第三问(祥见文末附件),并将评分标准作相应调整。
19.解:(1)∵----数学.files/image474.gif) ,其定义域为
,其定义域为----数学.files/image476.gif) ,
,
∴----数学.files/image478.gif) .……………………… 3分
.……………………… 3分
∵----数学.files/image480.gif) 是函数
是函数----数学.files/image482.gif) 的极值点,∴
的极值点,∴----数学.files/image484.gif) ,即
,即----数学.files/image486.gif) .
.
∵----数学.files/image488.gif) ,∴
,∴----数学.files/image490.gif) . ……………………… 6分
. ……………………… 6分
经检验当----数学.files/image490.gif) 时,
时,----数学.files/image480.gif) 是函数
是函数----数学.files/image482.gif) 的极值点,
的极值点,
∴----数学.files/image490.gif) .
……………………… 8分
.
……………………… 8分
(2)由题意,可知方程----数学.files/image494.gif) 在区间
在区间----数学.files/image496.gif) 上有根,因为
上有根,因为----数学.files/image498.gif) 在
在----数学.files/image496.gif) 上是单调减函数,
上是单调减函数,----数学.files/image500.gif) 在
在----数学.files/image496.gif) 上是单调增函数,……………………… 10分
上是单调增函数,……………………… 10分
所以,----数学.files/image502.gif) ……………………… 14分
……………………… 14分
----数学.files/image504.gif) ……………………… 16分
……………………… 16分
20.解:(1) ----数学.files/image506.gif) ┉┉┉┉┉┉2分
┉┉┉┉┉┉2分
----数学.files/image508.gif) ┉┉┉┉┉┉5分
┉┉┉┉┉┉5分
----数学.files/image510.gif)
----数学.files/image512.gif) ┉┉┉┉┉┉8分
┉┉┉┉┉┉8分
(2)----数学.files/image514.gif) ┉┉┉┉┉┉10分
┉┉┉┉┉┉10分
----数学.files/image516.gif)
----数学.files/image518.gif) ┉┉┉┉┉┉12分
┉┉┉┉┉┉12分
----数学.files/image520.gif)
----数学.files/image522.gif) ┉┉┉┉┉┉14分
┉┉┉┉┉┉14分
----数学.files/image524.gif) ┉┉┉┉┉┉16分
┉┉┉┉┉┉16分
附加题部分
A(1)证明:因为----数学.files/image526.gif) ,所以
,所以----数学.files/image528.gif)
又----数学.files/image245.gif) 是圆O的直径,所以
是圆O的直径,所以----数学.files/image531.gif)
又因为----数学.files/image533.gif) (弦切角等于同弧所对圆周角)……………………3分
(弦切角等于同弧所对圆周角)……………………3分
所以----数学.files/image535.gif) 所以
所以----数学.files/image537.gif)
又因为----数学.files/image539.gif) ,所以
,所以----数学.files/image541.gif) 相似
相似
所以----数学.files/image543.gif) ,即
,即----数学.files/image266.gif) ……………………5分
……………………5分
(2)解:因为----数学.files/image264.gif) ,所以
,所以----数学.files/image547.gif) ,
,
因为----数学.files/image262.gif) ,所以
,所以----数学.files/image550.gif)
由(1)知:----数学.files/image552.gif) 。所以
。所以----数学.files/image554.gif) ……………………8分
……………………8分
所以----数学.files/image556.gif) ,即圆的直径
,即圆的直径----数学.files/image558.gif)
又因为----数学.files/image560.gif) ,即
,即----数学.files/image562.gif)
解得----数学.files/image564.gif) ……………………10分
……………………10分
B.解:令----数学.files/image566.gif) 得到:
得到:----数学.files/image568.gif) ……………2分
……………2分
解得:----数学.files/image570.gif) ……………………6
……………………6
所以,矩阵A的特征值为2和3.
当----数学.files/image572.gif) ,
,----数学.files/image574.gif) 令
令----数学.files/image576.gif) 得
得----数学.files/image578.gif) ,
,
所以,对应的特征向量为----数学.files/image580.gif) ……………………8
……………………8
当----数学.files/image582.gif) ,
,----数学.files/image584.gif) 令
令----数学.files/image576.gif) 得
得----数学.files/image587.gif) ,所以,对应的特征向量为
,所以,对应的特征向量为----数学.files/image589.gif)
矩阵A的两个特征值分别是2和3,它们对应的特征向量分别是----数学.files/image580.gif) 和
和----数学.files/image589.gif) .…10分
.…10分
C.解:将直线----数学.files/image192.gif) 的参数方程化为普通方程为:
的参数方程化为普通方程为:----数学.files/image592.gif) ……………………2分
……………………2分
将圆C的极坐标方程化为普通方程为:----数学.files/image594.gif) ………………4分
………………4分
从圆方程中可知:圆心C(1,1),半径----数学.files/image596.gif) ,
,
所以,圆心C到直线----数学.files/image192.gif) 的距离
的距离----数学.files/image598.gif) …………6分
…………6分
所以直线----数学.files/image192.gif) 与圆C相交. ……………………7分
与圆C相交. ……………………7分
所以直线----数学.files/image192.gif) 被圆C截得的弦长为
被圆C截得的弦长为----数学.files/image601.gif) .……………………10分
.……………………10分
D.证明:要证原不等式成立,只须证:----数学.files/image603.gif)
即只须证:----数学.files/image605.gif)
由柯西不等式易知上式显然成立,所以原不等式成立.
22.解:(1)设“小明中一等奖”为事件B1 ,“小辉中一等奖”为事件B2 ,事件B1与事件B2相互独立,他们俩都中一等奖,则P(B1B2)=P(B1)P(B2)=0.0001
所以,购买两张这种彩票都中一等奖的概率为----数学.files/image607.gif) .………..3分
.………..3分
(2)设“购买一张这种彩票中一等奖”为事件A,“购买一张这种彩票中二等奖”为事件B,显然,事件A与事件B互斥,
所以,----数学.files/image609.gif) ……………………5分
……………………5分
故购买一张这种彩票能中奖的概率为0.1.……………………6分
(3)对应不中奖、中二等奖、中一等奖,----数学.files/image611.gif) 的分布列如下:
的分布列如下:
----数学.files/image613.gif)
----数学.files/image615.gif)
----数学.files/image617.gif)
----数学.files/image619.gif)
----数学.files/image621.gif)
----数学.files/image623.gif)
----数学.files/image625.gif)
----数学.files/image627.gif)
----数学.files/image629.gif) ……………………9分
……………………9分
购买一张这种彩票的期望收益为损失----数学.files/image631.gif) 元.……………………10分
元.……………………10分
23. 解:(1)设P(x,y),根据题意,得----数学.files/image633.gif) .………3分
.………3分
化简,得----数学.files/image635.gif) .……………………………………………4分
.……………………………………………4分
(2)设过Q的直线方程为----数学.files/image637.gif) ,代入抛物线方程,整理,得
,代入抛物线方程,整理,得----数学.files/image639.gif) .
.
∴△=----数学.files/image641.gif) .解得
.解得----数学.files/image643.gif) .………………………………………6分
.………………………………………6分
所求切线方程为----数学.files/image645.gif) (也可以用导数求得切线方程),
(也可以用导数求得切线方程),
此时切点的坐标为(2,1),(-2,1),且切点在曲线C上. …………8分
由对称性知所求的区域的面积为
----数学.files/image647.gif) .……………………………10分
.……………………………10分
附件:
第19题第3问:
(3)若对任意的----数学.files/image649.gif) 都有
都有----数学.files/image651.gif) 成立,求实数
成立,求实数----数学.files/image129.gif) 的取值范围.
的取值范围.
(3)对任意的----数学.files/image653.gif) 都有
都有----数学.files/image655.gif) ≥
≥----数学.files/image657.gif) 成立等价于对任意的
成立等价于对任意的----数学.files/image653.gif) 都有
都有----数学.files/image660.gif) ≥
≥----数学.files/image662.gif) .……………………… 7分
.……………………… 7分
当----数学.files/image125.gif)
----数学.files/image665.gif) [1,
[1,----数学.files/image229.gif) ]时,
]时,----数学.files/image668.gif) .
.
∴函数----数学.files/image670.gif) 在
在----数学.files/image672.gif) 上是增函数.
上是增函数.
∴----数学.files/image674.gif) .………………………9分
.………………………9分
∵----数学.files/image676.gif) ,且
,且----数学.files/image678.gif) ,
,----数学.files/image488.gif) .
.
①当----数学.files/image681.gif) 且
且
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com