
题目列表(包括答案和解析)
| 2x1+2x2 |
| 2 |
| x1+x2 |
| 2 |
| ||||
| 2 |
| x1+x2 |
| 2 |
已知O是△ABC内任意一点,连结AO、BO、CO并延长交对边于A′,B′,C′,则![]() +
+![]() +
+![]() =1,这是一道平面几何题,其证明常采用“面积法”.
=1,这是一道平面几何题,其证明常采用“面积法”.
![]() +
+![]() +
+![]() =
=![]() +
+![]() +
+![]() =
=![]() =1,
=1,
请运用类比思想,对于空间中的四面体V—BCD,存在什么类似的结论?并用体积法证明.
把函数 的图象按向量
的图象按向量 平移得到函数
平移得到函数 的图象.
的图象.
(1)求函数 的解析式; (2)若
的解析式; (2)若 ,证明:
,证明: .
.
【解析】本试题主要考查了函数 平抑变换和运用函数思想证明不等式。第一问中,利用设 上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入
上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入 ,便可以得到结论。第二问中,令
,便可以得到结论。第二问中,令 ,然后求导,利用最小值大于零得到。
,然后求导,利用最小值大于零得到。
(1)解:设 上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入
上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入 得y-2=ln(x+1)-2即y=ln(x+1),所以
得y-2=ln(x+1)-2即y=ln(x+1),所以 .……4分
.……4分
(2) 证明:令 ,……6分
,……6分
则 ……8分
……8分
 ,∴
,∴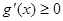 ,∴
,∴ 在
在 上单调递增.……10分
上单调递增.……10分
故 ,即
,即
已知点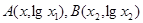 是函数
是函数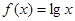 的图象上任意不同两点,依据图象可知,段段AB总是位于A,B两点之间函数图象的下方,因此有结论
的图象上任意不同两点,依据图象可知,段段AB总是位于A,B两点之间函数图象的下方,因此有结论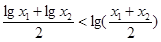 成立。运用类比思想方法可知,若点
成立。运用类比思想方法可知,若点 ,
, 是函数
是函数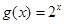 的图象上的不同两点,则类似地有成立 。
的图象上的不同两点,则类似地有成立 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com