
题目列表(包括答案和解析)
如图所示,直线l1和l2相交于点M,l1⊥l2,点N∈l1,以A、B为端点的曲线段C上任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=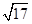 ,|AN|=3,且|NB|=6,建立适当的坐标系,求曲线段C的方程.
,|AN|=3,且|NB|=6,建立适当的坐标系,求曲线段C的方程.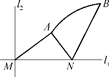
 ,|AN|=3,且|BN|=6,建立适当的坐标系,求曲线段C的方程.
,|AN|=3,且|BN|=6,建立适当的坐标系,求曲线段C的方程.
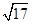 ,|AN|=3,且|NB|=6,建立适当的坐标系,求曲线段C的方程.
,|AN|=3,且|NB|=6,建立适当的坐标系,求曲线段C的方程.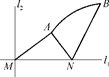
如图所示,直线l1和l2相交于点M,l1⊥l2,点N∈l1,以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=![]() ,|AN|=3,且|BN|=6,建立适当的坐标系,求曲线C的方程.
,|AN|=3,且|BN|=6,建立适当的坐标系,求曲线C的方程.

如图所示,直线l1和l2相交于点M,且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任意一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=![]() ,|AN|=3,且|BN|=6,分别以l1及l2为x轴和y轴,建立如图坐标系,求曲线C的方程.
,|AN|=3,且|BN|=6,分别以l1及l2为x轴和y轴,建立如图坐标系,求曲线C的方程.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com