练习册

  • 练习册
  • 试题
    体积V＝.评述:重点考查圆锥.圆锥的体积.异面直线的距离及三垂线定理的应用. 【查看更多】

     

    题目列表(包括答案和解析)

    直三棱柱ABC－A1B1C1的直观图及三视图如下图所示，D为AC的中点，则下列命题是假命题的是(   )

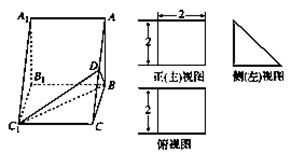
    A．AB1∥平面BDC1

    B．A1C⊥平面BDC1

    C．直三棱柱的体积V＝4

    D．直三棱柱的外接球的表面积为4π

     

    查看答案和解析>>

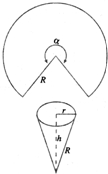    如图，用半径为R的圆铁皮，剪一个圆心角为α的扇形，制成一个圆锥形的漏斗，问圆心角α取什么值时，漏斗容积最大．（圆锥体积公式：V=
    13
    πr2h    ，其中圆锥的底面半径为r，高为h）

    查看答案和解析>>

    设一个圆锥的底面半径为r，高为h，母线为l．
    （1）若r=2，h=6，求圆锥的侧面积Mc，表面积Mb和体积V；
    （2）判断各种不同形状的圆锥，表达式
    (Mb-Mc)Mb(2Mc-Mb)V2
    是否为定值，并说明理由．

    查看答案和解析>>

    如图，已知一个圆锥的底面半径为R，高为h，在其中有一个高为x的内接圆柱（其中R，h均为常数）．
    （1）当x=
    23
    h时，求内接圆柱上方的圆锥的体积V；
    （2）当x为何值时，这个内接圆柱的侧面积最大？并求出其最大值．

    查看答案和解析>>

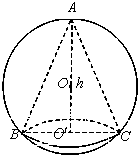    如图，已知球的半径为定值R，球内接圆锥的高为h（h＞R），体积为V，
    （1）写出以h表示V的函数关系式V（h）；
    （2）当h为何值时，V（h）有最大值，并求出该最大值．

    查看答案和解析>>


    同步练习册答案