
题目列表(包括答案和解析)
已知函数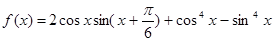
(1)求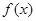 的最小正周期;
的最小正周期;
(2)若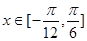 ,求
,求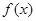 的最大值、最小值及相应的x的值。
的最大值、最小值及相应的x的值。
【解析】本试题主要是考查了三角函数的化简和变形,以及运用三角函数的性质求解最值问题的综合运用试题。
若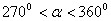 ,三角函数式
,三角函数式 的化简结果为( )
的化简结果为( )
A.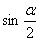 B.
B.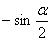 C.
C.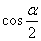 D.
D.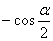
A.3.6=x是赋值语句
B.利用赋值语句可以进行代数式的化简
C.赋值语句中的等号与数学里的等号意义相同
D.赋值语句的作用是先计算出赋值号右边表达式的值,然后把该值赋给赋值号左边的变量,使该变量的值等于表达式的值.
先化简再计算:
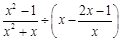 ,其中x是一元二次方程
,其中x是一元二次方程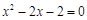 的正数根.
的正数根.
已知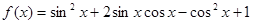
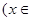 R
R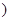 .
.
(1)求函数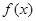 的最大值,并指出此时
的最大值,并指出此时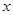 的值.
的值.
(2)若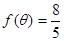 ,求
,求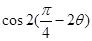 的值.
的值.
【解析】本试题主要考查了三角函数的性质的运用。(1)中,三角函数先化简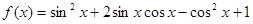 =
=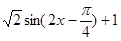 ,然后利用
,然后利用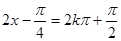 是,函数取得最大值
是,函数取得最大值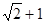 (2)中,结合(1)中的结论,然后由
(2)中,结合(1)中的结论,然后由
得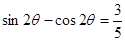 ,两边平方得
,两边平方得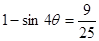 即
即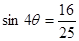 ,因此
,因此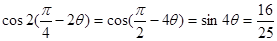
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com