
题目列表(包括答案和解析)
(本小题共13分)若有穷数列{an}满足:(1)首项a1=1,末项am=k,(2)an+1= an+1或an+1=2an ,(n=1,2,…,m-1),则称数列{an}为k的m阶数列.
(Ⅰ)请写出一个10的6阶数列;
(Ⅱ)设数列{bn}是各项为自然数的递增数列,若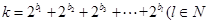 ,且
,且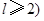 ,求m的最小值.
,求m的最小值.
(考生务必将答案答在答题卡上,在试卷上作答无效)
 如图直角梯形OABC中,∠COA=∠OAB=
如图直角梯形OABC中,∠COA=∠OAB=| π |
| 2 |
| SC |
| OB |
| n |
| n |
| n |
| k |
| k |
| SC |
| k |
| OB |
| k |
 [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
|
|
| π |
| 2 |
| π |
| 4 |
| a2+b2 |
| c2+d2 |
| (ac+bd)(ad+bc) |
由函数y=f(x)确定数列{an},an=f(n),函数y=f(x)的反函数y=f -1(x)能确定数列{bn},bn= f –1(n),若对于任意nÎN*,都有bn=an,则称数列{bn}是数列{an}的“自反数列”.
(1)若函数f(x)=![]() 确定数列{an}的自反数列为{bn},求an;
确定数列{an}的自反数列为{bn},求an;
(2)已知正数数列{cn}的前n项之和Sn=![]() (cn+
(cn+![]() ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论;
(3)在(1)和(2)的条件下,d1=2,当n≥2时,设dn=![]() ,Dn是数列{dn}的前n项之和,且Dn>log a (1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项之和,且Dn>log a (1-2a)恒成立,求a的取值范围.
参考答案
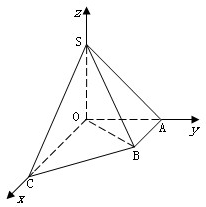
已知椭圆![]() =1,点P为其上一点,F1、F2为椭圆的焦点,Q为射线
=1,点P为其上一点,F1、F2为椭圆的焦点,Q为射线![]() 延长线上一点,且|PQ|=|PF2|,设R为F2Q的中点。
延长线上一点,且|PQ|=|PF2|,设R为F2Q的中点。
(1)当P点在椭圆上运动时,求R形成的轨迹方程;
(2)设点R形成的曲线为C,直线l:y=k(x+4![]() )与曲线C相交于A、B两点,若∠AOB=90o时,
)与曲线C相交于A、B两点,若∠AOB=90o时,
求k的值.
(请注意把答案填写在答题卡上)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com