
题目列表(包括答案和解析)
(本小题满分14分)已知函数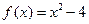 ,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n ÎN *),x1=4.
,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n ÎN *),x1=4.
(Ⅰ)用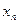 表示xn+1;
表示xn+1;
(Ⅱ)记an=lg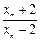 ,证明数列{an}成等比数列,并求数列{xn}的通项公式;
,证明数列{an}成等比数列,并求数列{xn}的通项公式;
(Ⅲ)若bn=xn-2,试比较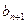 与
与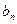 的大小.
的大小.
(本小题满分14分)已知函数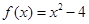 ,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n Î N *),x1=4.
,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n Î N *),x1=4.
(Ⅰ)用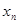 表示xn+1;
表示xn+1;
(Ⅱ)记an=lg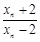 ,证明数列{an}成等比数列,并求数列{xn}的通项公式;
,证明数列{an}成等比数列,并求数列{xn}的通项公式;
(Ⅲ)若bn=xn-2,试比较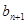 与
与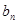 的大小.
的大小.
本题有(1)、(2)、(3)三个选考题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题记分.
(1)(本小题满分7分)选修4—2:矩阵与变换
已知二阶矩阵![]() 有特征值
有特征值![]() 及对应的一个特征向量
及对应的一个特征向量![]() .
.
(Ⅰ)求矩阵![]() ;
;
(Ⅱ)设曲线![]() 在矩阵
在矩阵![]() 的作用下得到的方程为
的作用下得到的方程为![]() ,求曲线
,求曲线![]() 的方程.
的方程.
(2)(本小题满分7分)选修4—4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),若圆
为参数),若圆![]() 在以该直角坐标系的原点
在以该直角坐标系的原点![]() 为极点、
为极点、![]() 轴的正半轴为极轴的极坐标系下的方程为
轴的正半轴为极轴的极坐标系下的方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点![]() 是曲线
是曲线![]() 上的动点,点
上的动点,点![]() 是圆
是圆![]() 上的动点,求
上的动点,求![]() 的最小值.
的最小值.
(3)(本小题满分7分)选修4—5:不等式选讲
已知函数![]() ,不等式
,不等式![]() 在
在![]() 上恒成立.
上恒成立.
(Ⅰ)求![]() 的取值范围;
的取值范围;
(Ⅱ)记![]() 的最大值为
的最大值为![]() ,若正实数
,若正实数![]() 满足
满足![]() ,求
,求![]() 的最大值.
的最大值.
本题有(1).(2).(3)三个选做题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.
(1)(本小题满分7分)选修4-2:矩阵与变换选做题
已知矩阵A= 有一个属于特征值1的特征向量
有一个属于特征值1的特征向量 .
.
(Ⅰ) 求矩阵A;
(Ⅱ) 矩阵B=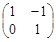 ,点O(0,0),M(2,-1),N(0,2),求
,点O(0,0),M(2,-1),N(0,2),求 在矩阵AB的对应变换作用下所得到的
在矩阵AB的对应变换作用下所得到的 的面积.
的面积.
(2)(本小题满分7分)选修4-4:坐标系与参数方程选做题
在直角坐标平面内,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系.已知曲线 的参数方程为
的参数方程为 ,曲线
,曲线 的极坐标方程为
的极坐标方程为 .
.
(Ⅰ)将曲线 的参数方程化为普通方程;(Ⅱ)判断曲线
的参数方程化为普通方程;(Ⅱ)判断曲线 与曲线
与曲线 的交点个数,并说明理由.
的交点个数,并说明理由.
(3)(本小题满分7分)选修4-5:不等式选讲选做题
已知函数 ,不等式
,不等式 在
在 上恒成立.
上恒成立.
(Ⅰ)求 的取值范围;
的取值范围;
(Ⅱ)记 的最大值为
的最大值为 ,若正实数
,若正实数 满足
满足 ,求
,求 的最大值.
的最大值.
本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题记分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.作
(1)选修4—2:矩阵与变换
若二阶矩阵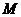 满足
满足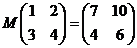 .
.
(Ⅰ)求二阶矩阵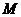 ;
;
(Ⅱ)把矩阵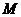 所对应的变换作用在曲线
所对应的变换作用在曲线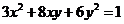 上,求所得曲线的方程.
上,求所得曲线的方程.
(2)选修4-4:坐标系与参数方程
已知在直角坐标系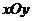 中,曲线
中,曲线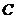 的参数方程为
的参数方程为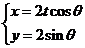 (t为非零常数,
(t为非零常数,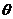 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系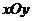 取相同的长度单位,且以原点
取相同的长度单位,且以原点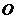 为极点,以
为极点,以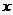 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线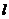 的方程为
的方程为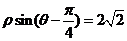 .
.
(Ⅰ)求曲线C的普通方程并说明曲线的形状;
(Ⅱ)是否存在实数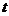 ,使得直线
,使得直线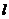 与曲线C有两个不同的公共点
与曲线C有两个不同的公共点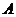 、
、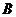 ,且
,且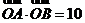 (其中
(其中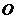 为坐标原点)?若存在,请求出;否则,请说明理由.
为坐标原点)?若存在,请求出;否则,请说明理由.
(3)选修4—5:不等式选讲
已知函数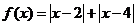 的最小值为
的最小值为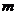 ,实数
,实数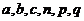 满足
满足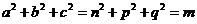 .
.
(Ⅰ)求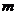 的值;
的值;
(Ⅱ)求证: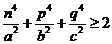 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com