
题目列表(包括答案和解析)
 的焦点为F1和F2,过点F1的直线l交椭圆于P,Q两点,且
的焦点为F1和F2,过点F1的直线l交椭圆于P,Q两点,且 ,
,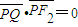 ,则椭圆的离心率为( )
,则椭圆的离心率为( )

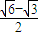

 的焦点为F1和F2,过点F1的直线l交椭圆于P,Q两点,且
的焦点为F1和F2,过点F1的直线l交椭圆于P,Q两点,且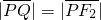 ,
,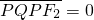 ,则椭圆的离心率为
,则椭圆的离心率为
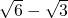
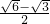
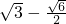
椭圆 ![]() 的焦点为F1和F2,过点F1的直线l交椭圆于P、Q两点,
的焦点为F1和F2,过点F1的直线l交椭圆于P、Q两点,![]() ,则椭圆的离心率为( )
,则椭圆的离心率为( )
(1)求椭圆的方程;
(2)设A1、A2分别是椭圆的左顶点和右顶点,P是椭圆上满足|PA1|-|PA2|=2的一点,求tan∠A1PA2的值;
(3)若过点(1,0)的直线与以原点为顶点、A2为焦点的抛物线相交于点M、N,求MN中点Q的轨迹方程.
 的焦点分别为F1和F2,过原点O作直线与椭圆相交于A,B两点.若△ABF2的面积是20,则直线AB的方程是 .
的焦点分别为F1和F2,过原点O作直线与椭圆相交于A,B两点.若△ABF2的面积是20,则直线AB的方程是 .湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com