
题目列表(包括答案和解析)
设函数f(x)=ax![]() +bx+1(a,b为实数),F(x)=
+bx+1(a,b为实数),F(x)=![]()
(1)若f(-1)=0且对任意实数x均有f(x)![]() 成立,求F(x)表达式。
成立,求F(x)表达式。
(2)在(1)的条件下,当x![]() 时,g(x)=f(x)-kx是单调函数,求实数k的取值范围。
时,g(x)=f(x)-kx是单调函数,求实数k的取值范围。
(3)(理)设m>0,n<0且m+n>0,a>0且f(x)为偶函数,求证:F(m)+F(n)>0。
设函数f(x)=x2-4x+3,g(x)=3x-2,集合M={x∈R|f(g(x))>0},N={x∈R|g(x)<2},则M∩N为( )
(A)(1,+∞) (B)(0,1)
(C)(-1,1) (D)(-∞,1)
已知函数f(x)在(-∞,0)∪(0,+∞)上有定义,且在(0,+∞)上是增函数,f(1)=0,又g(θ)=sin2θ-mcosθ-2m,θ∈[0,![]() ],设M={m|g(θ)<0,m∈R},N={m|f[g(θ)]<0},求M∩N.
],设M={m|g(θ)<0,m∈R},N={m|f[g(θ)]<0},求M∩N.
已知二次函数f(x)=ax2+bx,且f(x+1)为偶函数,定义:满足f(x)=x的实数x称为函数f(x)的不动点,若函数f(x)有且仅有一个不动点,
(1)求f(x)的解析式;
(2) 若函数g(x)= f(x)+![]() +
+![]() x2在 (0,
x2在 (0,![]() ]上是单调减函数,求实数k的取值范围;
]上是单调减函数,求实数k的取值范围;
(3)在(2)的条件下,是否存在区间[m,n](m<n),使得f(x)在区间[m,n]上的值域为[km,kn]?若存在,请求出区间[m,n];若不存在,请说明理由。
已知二次函数f(x)=ax2+bx,且f(x+1)为偶函数,定义:满足f(x)=x的实数x称为函数f(x)的“不动点”,若函数f(x)有且仅有一个不动点,
(1)求f(x)的解析式;
(2)若函数g(x)= f(x)+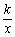 +
+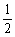 x2在 (0,
x2在 (0, ]上是单调减函数,求实数k的取值范围;
]上是单调减函数,求实数k的取值范围;
(3)在(2)的条件下,是否存在区间[m,n](m<n),使得f(x)在区间[m,n]上的值域为[km,kn]?若存在,请求出区间[m,n];若不存在,请说明理由。
′
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com