（本小题满分9分）

在一个特定时段内，以点E为中心的10海里以内海域被设为警戒水域.点E正北40海里处有一个雷达观测站A，某时刻测得一艘匀速直线行驶的船只位于点A北偏东30°且与点A相距100海里的位置B，经过2小时又测得该船已行驶到点A北偏东60°且与点A相距20海里的位置C.

（I）求该船的行驶速度（单位：海里/小时）;

（II）若该船不改变航行方向继续行驶.判断

它是否会进入警戒水域，并说明理由.

（本小题满分9分）
在一个特定时段内，以点E为中心的10海里以内海域被设为警戒水域.点E正北40海里处有一个雷达观测站A，某时刻测得一艘匀速直线行驶的船只位于点A北偏东30°且与点A相距100海里的位置B，经过2小时又测得该船已行驶到点A北偏东60°且与点A相距20海里的位置C.
（I）求该船的行驶速度（单位：海里/小时）;
（II）若该船不改变航行方向继续行驶.判断
它是否会进入警戒水域，并说明理由.

（本小题满分13分）某沿海地区养殖的一种特色海鲜上市时间仅能持续5个月，预测上市初期和后期会因供应不足使价格呈持续上涨态势，而中期又将出现供大于求，使价格连续下跌．现有三种价格模拟函数：①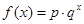；②；③．（以上三式中均为常数，且）

（1）为准确研究其价格走势，应选哪种价格模拟函数(不必说明理由)

（2）若，，求出所选函数的解析式（注：函数定义域是．其中表示8月1日，表示9月1日，…，以此类推）；

（3）在（2）的条件下研究下面课题：为保证养殖户的经济效益，当地政府计划在价格下跌期间积极拓宽外销，请你预测该海鲜将在哪几个月份内价格下跌．

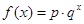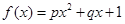（本小题满分13分）某沿海地区养殖的一种特色海鲜上市时间仅能持续5个月，预测上市初期和后期会因供应不足使价格呈持续上涨态势，而中期又将出现供大于求，使价格连续下跌．现有三种价格模拟函数：①；②；③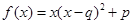．（以上三式中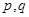均为常数，且）
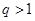（1）为准确研究其价格走势，应选哪种价格模拟函数(不必说明理由)
（2）若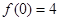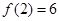，，求出所选函数的解析式（注：函数定义域是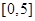．其中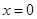表示8月1日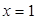，表示9月1日，…，以此类推）；
（3）在（2）的条件下研究下面课题：为保证养殖户的经济效益，当地政府计划在价格下跌期间积极拓宽外销，请你预测该海鲜将在哪几个月份内价格下跌．