
题目列表(包括答案和解析)
(13分)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两个不同的点,与
两个不同的点,与![]() 轴相交于点
轴相交于点![]() 。
。
(1)证明:![]() ;
;
![]() (2)若
(2)若![]() 是椭圆的一个焦点,且
是椭圆的一个焦点,且![]() ,求椭圆的方程。
,求椭圆的方程。
设直线![]() 与椭圆
与椭圆![]() 相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点.
相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点.
(1)证明:![]() ;
;
(2)若![]() 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程.
已知动直线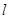 与椭圆
与椭圆
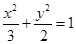 交于
交于
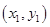 、
、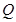
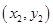 两不同点,且△
两不同点,且△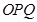 的面积
的面积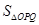 =
=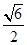 ,其中
,其中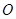 为坐标原点.
为坐标原点.
(1)证明 和
和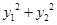 均为定值;
均为定值;
(2)设线段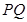 的中点为
的中点为 ,求
,求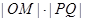 的最大值;
的最大值;
(3)椭圆 上是否存在点
上是否存在点 ,使得
,使得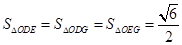 ?若存在,判断△
?若存在,判断△ 的形状;若不存在,请说明理由.
的形状;若不存在,请说明理由.
已知动直线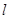 与椭圆
与椭圆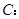
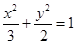 交于
交于
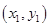 、
、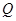
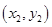 两不同点,且△
两不同点,且△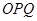 的面积
的面积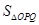 =
=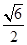 ,其中
,其中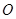 为坐标原点.
为坐标原点.
(1)证明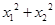 和
和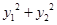 均为定值;
均为定值;
(2)设线段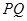 的中点为
的中点为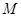 ,求
,求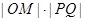 的最大值;
的最大值;
(3)椭圆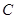 上是否存在点
上是否存在点 ,使得
,使得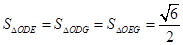 ?若存在,判断△
?若存在,判断△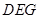 的形状;若不存在,请说明理由.
的形状;若不存在,请说明理由.
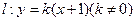 与椭圆
与椭圆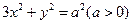 相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点.
相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点.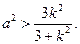 ;
;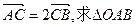 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程.一、选择题:(每题5分,共60分)
|