（2007•上海模拟）（1）若直角三角形两直角边长之和为12，求其周长p的最小值；
（2）若三角形有一个内角为arccos

7

9

，周长为定值p，求面积S的最大值；
（3）为了研究边长a，b，c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值，现有解法如下：16S²=（a+b+c）（a+b-c）（a-b+c）（-a+b+c）=[（a+b）²-c²][c²-（a-b）²]=-c⁴+2（a²+b²）c²-（a²-b²）²=-[c²-（a²+b²）]²+4a²b²
而-[c²-（a²+b²）]²≤0，a²≤81，b²≤64，则S≤36，但是，其中等号成立的条件是c²=a²+b²，a=9，b=8，于是c²=145与3≤c≤4矛盾，所以，此三角形的面积不存在最大值．
以上解答是否正确？若不正确，请你给出正确的答案．
（注：16S²=（a+b+c）（a+b-c）（a-b+c）（-a+b+c）称为三角形面积的海伦公式，它已经被证明是正确的）

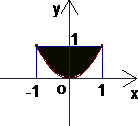利用计算机随机模拟方法计算图中阴影面积（如图所示）
第一步：利用计算机产生两个0～1区间的均匀随机数，x，y，其中-1＜x＜1，0＜y＜1；
第二步：拟（x，y）为点的坐标．共做此实验N次．若落在阴影部分的点的个数为N₁，
则可以计算阴影部分的面积S．例如：做了2000次实验，即N=2000，模拟得到N₁=1396，所以S=．

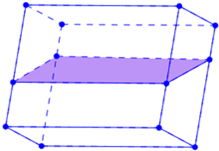如图，在透明塑料制成的长方体ABCD-A₁B₁C₁D₁容器内装进一些水，将容器底面一边BC固定于底面上，再将容器倾斜，随着倾斜度的不同，有下列三个说法：①水的形状始终是棱柱形状；②水面形成的四边形EFGH的面积不改变；③当E∈AA₁时，AE+BF是定值．其中正确说法是．（写出所以正确说法的序号）