题目列表(包括答案和解析)
（本小题满分14分）
设
是定义在[-1，1]上的偶函数，
的图象与的图象关于直线
对称，且当x∈[ 2，3 ] 时，
222233．
（1）求的解析式；
（2）若在
上为增函数，求
的取值范围；
（3）是否存在正整数，使的图象的最高点落在直线
上？若存在，求出的值；若不存在，请说明理由．
（本小题满分14分）
设关于
的函数
，其中
为
上的常数，若函数
在
处取得极大值
．
(Ⅰ)求实数的值；
(Ⅱ)若函数的图象与直线
有两个交点，求实数
的取值范围；
(Ⅲ)设函数
，若对任意地
，
恒成立，求实数
的取值范围.
（本小题满分14分）
已知：函数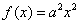
（
），
．
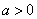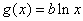（1）若函数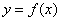
图象上的点到直线
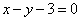距离的最小值为
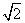，求
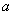的值；
（2）关于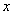
的不等式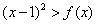
的解集中的整数恰有3个，求实数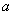的取值范围；
（3）对于函数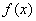
与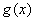
定义域上的任意实数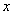，若存在常数
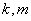，使得不等式
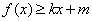和
都成立，则称直线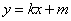
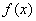为函数与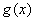的“分界线”。设
，
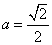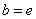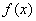，试探究与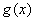是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
（本小题满分14分）
已知关于x的函数
，其导函数
.
（1）如果函数
试确定b、c的值；
（2）设当
时，函数
的图象上任一点P处的切线斜率为k，若
，求实数b的取值范围。
（本小题满分14分）某公司试销一种成本单价为500元的新产品，规定试销时销售单价不低于成本单价，又不高于800元．经试销调查，发现销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y＝kx＋b(k≠0)，函数图象如图所示．
(1)根据图象，求一次函数y＝kx＋b(k≠0)的表达式；
(2)设公司获得的毛利润(毛利润＝销售总价－成本总价)为S元．试问销售单价定为多少时，该公司可获得最大毛利润？最大毛利润是多少？此时的销售量是多少？
题号
答案
1.解析：命题“
”的否命题是：“
”，故选C．
2.解析：由已知，得：
，故选．
3.解析：若
，则
，解得
．故选．
4.解析：由题意得
，又
．
故选．
5.解析：设成绩为环的人数是
，由平均数的概念，得：
．
故选．
6.解析：是偶函数；是指数函数；是对数函数．故选．
7.解析：①的三视图均为正方形；②的三视图中正视图．侧视图为相同的等腰三角形，俯视图为圆；④的三视图中正视图．侧视图为相同的等腰三角形，俯视图为正方形．故选．
8.解析：程序的运行结果是
，选．
9.解析：
的图象先向左平移
，横坐标变为原来的倍
．答案：．
10.解析：特殊值法：令
，有
．故选．
题号
11
12
13
14
15
答案
11.解析：
．
12.解析：令
，则
，令
，则
，
同理得
即当
时，
的值以为周期，
所以
．
13.解析：由图象知：当函数
的图象过点
时，
取得最大值为2．
14. (坐标系与参数方程选做题)解析：将极坐标方程转化成直角坐标方程，圆
上的动点到直线
的距离的最大值就是圆心
到直线的距离
再加上半径
．故填．
15. (几何证明选讲选做题)解析：连结
，
则在
和
中：
，
且
，所以
，
故
．
三．解答题：本大题共6小题，满分80分．解答须写出文字说明．证明过程和演算步骤．
16.析：主要考察三角形中的边角关系、向量的坐标运算、二次函数的最值．
解：(Ⅰ)∵
，∴
， ………………3分
又∵
，∴
． ……………………………………………5分
（Ⅱ）
……………………………………………6分
， ………………………8分
∵
，∴
． ……………10分
∴当
时，取得最小值为
． …………12分
17．析：主要考察立体几何中的位置关系、体积．
解：(Ⅰ)证明：连结
，则//
， …………1分
∵
是正方形，∴
．∵
面，∴
．
又
，∴
面
． ………………4分
∵
面，∴
，
∴
． …………………………………………5分
（Ⅱ）证明：作
的中点F，连结
．
∵
是
的中点，∴
，
∴四边形
是平行四边形，∴ 
． ………7分
∵
是的中点，∴
，
又
，∴
．
∴四边形
是平行四边形，
//
，
∵
，
，
∴平面
面
． …………………………………9分
又
平面
，∴
面． ………………10分
（3）
． ……………………………11分
． ……………………………14分
18．析：主要考察事件的运算、古典概型．
解：设“朋友乘火车、轮船、汽车、飞机来”分别为事件
，则
，
，
，
，且事件之间是互斥的．
(Ⅰ)他乘火车或飞机来的概率为
………4分
(Ⅱ)他乘轮船来的概率是，
所以他不乘轮船来的概率为
． ………………8分
（Ⅲ)由于
，
所以他可能是乘飞机来也可能是乘火车或汽车来的． …………………12分
19.析：主要考察函数的图象与性质，导数的应用．
解：(Ⅰ)由函数
的图象关于原点对称，得
，………………1分
∴
，∴
． …………2分
∴
，∴
． ……………………………4分
∴
，即
． ……………………6分
∴
． ……………………………………………………7分
(Ⅱ)由(Ⅰ)知
，∴
．
由
，∴
． …………………9分
0
+
0
ㄋ
极小
ㄊ
极大
ㄋ
∴
． ………………………14分
20．析：主要考察直线．圆的方程，直线与圆的位置关系．
解：(Ⅰ)（法一）∵点
在圆
上， …………………………2分
∴直线
的方程为
，即
． ……………………………5分
（法二）当直线垂直轴时，不符合题意． ……………………………2分
当直线与轴不垂直时，设直线的方程为
，即
．
则圆心
到直线的距离
，即：
，解得
，……4分
∴直线的方程为． ……………………………………………5分
（Ⅱ）设圆
：
，∵圆过原点，∴
．
∴圆的方程为
．…………………………7分
∵圆被直线
截得的弦长为
，∴圆心
到直线：的距离：
． …………………………………………9分
整理得：
，解得
或
． ……………………………10分
∵
，∴． …………………………………………………………13分
∴圆：
． ……………………………………14分
21．析：主要考察等差、等比数列的定义、式，求数列的和的方法．
解：(Ⅰ)设
的公差为，则：
，
，
∵
，
，∴
，∴
． ………………………2分
∴
． …………………………………………4分
（Ⅱ）当
时，
，由
，得
． …………………5分
当
时，
，
，
∴
，即
． …………………………7分
∴
． ……………………………………………………………8分
∴
是以
为首项，为公比的等比数列． …………………………………9分
（Ⅲ）由（2）可知：
． ……………………………10分
∴
． …………………………………11分
∴
．
∴
．
∴
． ………………………………………13分
∴
． …………………………………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com