
(Ⅱ)求四棱锥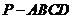 的体积.
的体积.
 (Ⅰ)设
(Ⅰ)设 是
是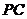 上的一点,证明:平面
上的一点,证明:平面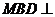 平面
平面 ;
;
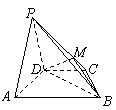
51.如图,在四棱锥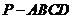 中,平面
中,平面 平面
平面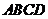 ,
,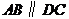 ,
,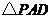 是等边三角形,已知
是等边三角形,已知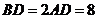 ,
,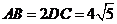 .
.
又EF∩CF=F,
∴BD⊥面EFC,∵BD 面BCD,∴面
面BCD,∴面 面
面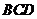
∵EF∥ 面ACD,AD
面ACD,AD 面ACD,∴直线EF∥面ACD;
面ACD,∴直线EF∥面ACD;
(2)∵AD⊥BD,EF∥AD,∴EF⊥BD,
∵CB=CD,F是BD的中点,∴CF⊥BD
证: (1)∵E,F分别是 的中点.
的中点.
∴EF是△ABD的中位线,∴EF∥AD,
求证:(1)直线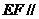 面
面 ;
; (2)平面
(2)平面 面
面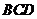 .
.
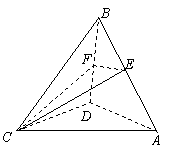
50.如图,在四面体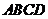 中,
中,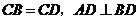 ,点
,点 分别是
分别是 的中点.
的中点.
 解:从三视图可以看出该几何体是由一个球和一个圆柱组合而成的,其表面及为
解:从三视图可以看出该几何体是由一个球和一个圆柱组合而成的,其表面及为 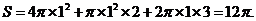
十六。点、线、面之间的位置关系(平面及及基本性质A;直线与平面平行、垂直的判定与性质B;两平面平行、垂直的判定与性质B)
49.右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com