
A s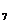 B s
B s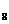 C s
C s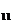 D s
D s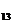
正确答案: D 错因:学生对等差数列通项公式的逆向使用和等差数列的性质不能灵活应用。
2.(石庄中学)已知s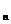 是等差数列{a
是等差数列{a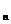 }的前n项和,若a
}的前n项和,若a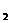 +a
+a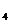 +a
+a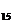 是一个确定的常数,则数列{s
是一个确定的常数,则数列{s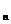 }中是常数的项是( )
}中是常数的项是( )
正确答案:D 错因:学生不能运用数列的性质计算a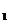 +a
+a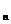 =
=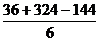
1.(石庄中学)设s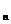 是等差数列{a
是等差数列{a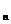 }的前n项和,已知s
}的前n项和,已知s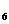 =36,
=36, s
s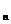 =324, s
=324, s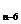 =144 (n>6),则n=( )
=144 (n>6),则n=( )
A 15 B
∴ 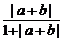 ≤
≤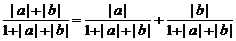 ≤
≤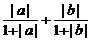 ①
①
错因:①的推理无根据。
=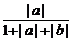 +
+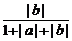 ≤
≤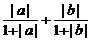
点评:错证:∵|a+b|≤|a|+|b|
∴ 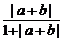 =
=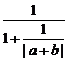 ≤
≤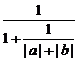 =
=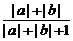
12.(蒲中)设a、b∈R,求证: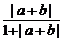 ≤
≤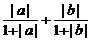
证明:当|a+b|=0时,不等式已成立
当|a+b|≠0时,∵ |a+b|≤|a|+|b|
11.(城西中学)在边长为a的正三角形中,点P、Q、R分别在BC、CA、AB上,且BP+CQ+AR=a,设BP=x,CQ=y,AR=z,三角形PQR的面积为s,求s的最大值及相应的x、y、z的值。
解 设ΔBPR、ΔPCR、ΔARQ的面积为s1、、s2、s3,则
S=SΔABC-S1-S2-S3=a2-[a2-(xy+xz+yz)]=(xy+xz+yz)
由x+y+z=a,得xy+yz+zx≤,∴Smav=a2,此时,x=y=z=
错因:不知如何使用基本不等式。
10.(城西中学)设集合M=[-1,1],N=[-,],f(x)=2x2+mx-1,若x∈N,m∈M,求证|f(x)|≤
证明:|f(x)|=|2x2+mx-1|= |(2x2-1)+mx|≤|(2x2-1)|+|mx|= (2x2-1)+|mx|≤(2x 2-1)+| x|
=-2(| x|-)2+≤
错因:不知何时使用绝对值不等式。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com