
9. (宁夏海南6)设x,y满足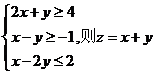
(A)有最小值2,最大值3 (B)有最小值2,无最大值
(C)有最大值3,无最小值 (D)既无最小值,也无最大值
解析:画出可行域可知,当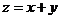 过点(2,0)时,
过点(2,0)时,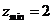 ,但无最大值。选B.
,但无最大值。选B.
8. (广东18) 14.(不等式选讲选做题)不等式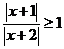 的实数解为 .
的实数解为 .
[解析]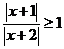
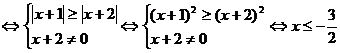 且
且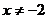 .
.
7. (浙江13)若实数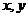 满足不等式组
满足不等式组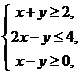 则
则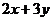 的最小值是
.
的最小值是
.
答案:4
解析:通过画出其线性规划,可知直线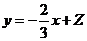 过点
过点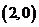 时,
时,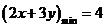
6.(山东13) 不等式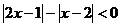 的解集为
.
的解集为
.
[解析]:原不等式等价于不等式组①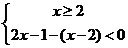 或②
或②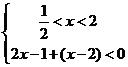
或③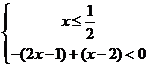 不等式组①无解,由②得
不等式组①无解,由②得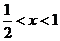 ,由③得
,由③得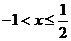 ,综上得
,综上得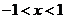 ,所以原不等式的解集为
,所以原不等式的解集为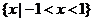 .
. 

答案: 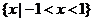
[命题立意]:本题考查了含有多个绝对值号的不等式的解法,需要根据绝对值的定义分段去掉绝对值号,最后把各种情况综合得出答案.本题涉及到分类讨论的数学思想.
5.(山东12)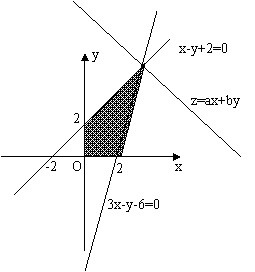 设x,y满足约束条件
设x,y满足约束条件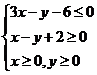 ,
, 

若目标函数z=ax+by(a>0,b>0)的值是最大值为12,
则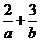 的最小值为( ).
的最小值为( ).
A.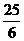 B.
B.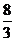 C.
C. 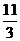 D.
4
D.
4
[解析]:不等式表示的平面区域如图所示阴影部分,当直线ax+by= z(a>0,b>0)
过直线x-y+2=0与直线3x-y-6=0的交点(4,6)时,
目标函数z=ax+by(a>0,b>0)取得最大12,
即4a+6b=12,即2a+3b=6, 而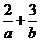 =
=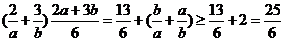 ,故选A.
,故选A.
答案:A
[命题立意]:本题综合地考查了线性规划问题和由基本不等式求函数的最值问题.要求能准确地画出不等式表示的平面区域,并且能够求得目标函数的最值,对于形如已知2a+3b=6,求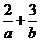 的最小值常用乘积进而用基本不等式解答.
的最小值常用乘积进而用基本不等式解答. 

4.(天津10)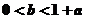 ,若关于x 的不等式
,若关于x 的不等式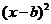 >
>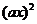 的解集中的整数恰有3个,则
的解集中的整数恰有3个,则
(A)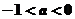 (B)
(B)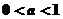 (C)
(C)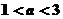 (D)
(D)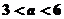
[考点定位]本小题考查解一元二次不等式,
解析:由题得不等式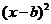 >
>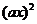 即
即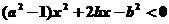 ,它的解应在两根之间,故有
,它的解应在两根之间,故有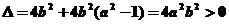 ,不等式的解集为
,不等式的解集为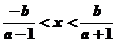 或
或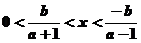 。若不等式的解集为
。若不等式的解集为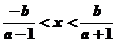 ,又由
,又由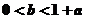 得
得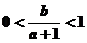 ,故
,故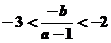 ,即
,即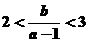
3.(天津6)设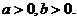 若
若 的最小值为
的最小值为
A 8
B 4 C
1 D 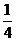
[考点定位]本小题考查指数式和对数式的互化,以及均值不等式求最值的运用,考查了变通能力。
[解析]因为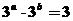 ,所以
,所以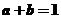 ,
,
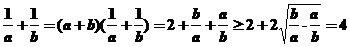 ,当且仅当
,当且仅当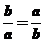 即
即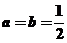 时“=”成立,故选择C
时“=”成立,故选择C
2.(天津2)设变量x,y满足约束条件: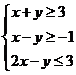 .则目标函数z=2x+3y的最小值为
.则目标函数z=2x+3y的最小值为
(A)6 (B)7 (C)8 (D)23
 [考点定位]本小考查简单的线性规划,基础题。
[考点定位]本小考查简单的线性规划,基础题。
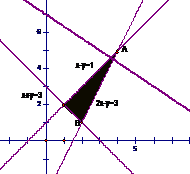
解析:画出不等式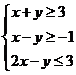 表示的可行域,如右图,
表示的可行域,如右图,
让目标函数表示直线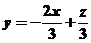 在可行域上平移,知在点B自目标函数取到最小值,解方程组
在可行域上平移,知在点B自目标函数取到最小值,解方程组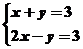 得
得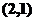 ,所以
,所以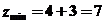 ,故选择B。
,故选择B。
1. (安徽7)若不等式组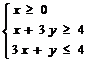 所表示的平面区域被直线
所表示的平面区域被直线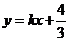 分为面积相等的两部分,则
分为面积相等的两部分,则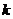 的值是
的值是

 (A)
(A)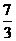 (B)
(B)
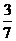 (C)
(C)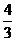 (D)
(D)
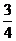

[解析]:不等式表示的平面区域如图所示阴影部分△ABC
由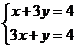 得A(1,1),又B(0,4),C(0,
得A(1,1),又B(0,4),C(0,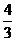 )
)
∴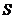 △ABC=
△ABC=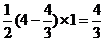 ,设
,设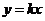 与
与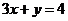 的
的
交点为D,则由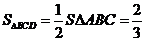 知
知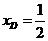 ,∴
,∴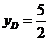
∴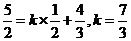 选A。
选A。
22.(本小题满分14分)
根据定义在集合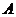 上的函数
上的函数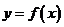 ,构造一个数列发生器,其工作原理如下:
,构造一个数列发生器,其工作原理如下:
①输入数据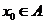 ,计算出
,计算出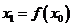 ;
;
②若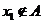 ,则数列发生器结束工作;若
,则数列发生器结束工作;若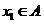 ,则输出
,则输出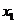 ,并将
,并将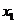 反馈回输入端,再计算出
反馈回输入端,再计算出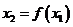 ,并依此规律继续下去.
,并依此规律继续下去.
若集合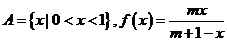
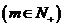 .
.
(Ⅰ)求证:对任意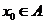 ,此数列发生器都可以产生一个无穷数列
,此数列发生器都可以产生一个无穷数列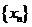 ;
;
(Ⅱ)若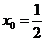 ,记
,记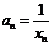 ,求数列
,求数列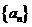 的通项公式;
的通项公式;
(Ⅲ)在(Ⅱ)的条件下,证明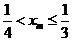 .
.
成都市2010届高中毕业班摸底测试
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com