
10.设函数 ,则
,则 =____.
=____.
9.下列函数中,与函数 相同的函数是( )
相同的函数是( )
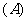






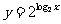
8.给定映射 ,点
,点 的原象是_______
的原象是_______
7.已知集合 ,映射
,映射 ,在
,在 作用下点
作用下点 的象是
的象是 ,则集合
,则集合 ( )
( )
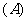







6.(1)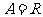 ,
, ,
, ;
;
(2) ,
, ,
, ;
;
(3) ,
, ,
, .
.
上述三个对应_____是 到
到 的映射.
的映射.
4.与函数y= 的图象相同的函数是 ( )
的图象相同的函数是 ( )
A y=2x-1(x>1/2) B
y=2x-1(x>1/2) B y=1/(2x-1) C
y=1/(2x-1) C y=1/(2x-1)(x>1/2) D
y=1/(2x-1)(x>1/2) D y=1/|2x-1|
y=1/|2x-1|
5 设函数f(x)=ax3+bx2+cx+d的图象如图所示,
设函数f(x)=ax3+bx2+cx+d的图象如图所示,
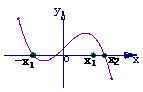 则f(-1)+f(1)( )
则f(-1)+f(1)( )
A 大于0 B
大于0 B 小于0
小于0
C 等于0 D
等于0 D 以上结论都不对
以上结论都不对
3.已知集合A={1,2,3,4},B={-1,1,2},
(1)集合A到B的映射共有多少个?
(2)若集合B中的每一个元素都有原象,这样的映射共有多少个?
(3)若集合B中元素2必须要有原象,这样的映射共有多少个?
2.设集合A={-1,0,1},B={2,3,4,5,6},映射A®B,使对任意xÎA,都有x+f(x)+xf(x)是奇数,则这样的映射f 的个数是
1.设f:A®B是从A到B的一个映射,其中A=B={(x,y)|xÎR,yÎR},f:(x,y)®(x+y,xy),则A中(1,-2)的象是 ,B中(1,-2)的原象是
6.复合函数:若y=f(u),u=g(x),xÎ(a,b),uÎ(m,n),那么y=f[g(x)]称为复合函数,u称为中间变量,它的取值范围是g(x)的值域
题型讲解
例1设集合 ,
, ,如果从
,如果从 到
到 的映射
的映射 满足条件:对
满足条件:对 中的每个元素
中的每个元素 与它在
与它在 中的象
中的象 的和都为奇数,则映射
的和都为奇数,则映射 的个数是(
的个数是(  )
)
A 8个
B
8个
B 12个 C
12个 C 16个 D
16个 D 18个
18个
解:∵ 为奇数,∴当
为奇数,∴当 为奇数
为奇数 、
、 时,它们在
时,它们在 中的象只能为偶数
中的象只能为偶数 、
、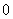 或
或 ,由分步计数原理和对应方法有
,由分步计数原理和对应方法有 种;而当
种;而当 时,它在
时,它在 中的象为奇数
中的象为奇数 或
或 ,共有
,共有 种对应方法.故映射
种对应方法.故映射 的个数是
的个数是 .故选D
.故选D
例2 集合A={3,4},B={5,6,7},那么可建立从A到B的映射个数是__________,从B到A的映射个数是__________
解:从A到B可分两步进行:第一步A中的元素3可有3种对应方法(可对应5或6或7),第二步A中的元素4也有这3种对应方法 由乘法原理,不同的映射种数N1=3×3=9
由乘法原理,不同的映射种数N1=3×3=9 反之从B到A,道理相同,有N2=2×2×2=8种不同映射
反之从B到A,道理相同,有N2=2×2×2=8种不同映射
答案:9 8
例3 A={1,2,3,4,5},B={6,7,8}从集合A到B的映射中满足f(1)≤f(2)≤f(3)≤f(4)≤f(5)的映射有( )
A 27
B
27
B 9
C
9
C 21 D
21 D 12
12
解:(1)当全是等号时,(即与B中的一个元素对应),则f有C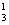 个;
个;
(2)有一个不等号时的映射(即与B中的两个元素对应),f有C ·C
·C =12个;
=12个;
(3)有二个不等号的映射,f有C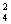 ·C
·C =6个
=6个
所以共有3+12+6=21个,答案选C
另一种解释法:将元素1,2,3,4,5按照从小到大的顺序串成一串之间有4个节点
若只有一个象就让这一串整体对应有C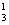 =3种方法;
=3种方法;
若恰有两个象就将这一串分为两段,并按照大小顺序对应,有C ·C
·C =12种方法;
=12种方法;
若恰有三个象就将这一串分为三段,并按照大小顺序对应,有C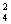 ·C
·C =6种方法
=6种方法
根据分类计数原理,共有3+12+6=21个映射 故选C
故选C
例4 试判断以下各组函数是否表示同一函数?
(1)f(x)= ,g(x)=
,g(x)= ;
;
(2)f(x)= ,g(x)=
,g(x)=
(3)f(x)= ,g(x)=(
,g(x)=( )2n-1(n∈N*);
)2n-1(n∈N*);
(4)f(x)=
 ,g(x)=
,g(x)= ;
;
(5)f(x)=x2-2x-1,g(t)=t2-2t-1
剖析:对于两个函数y=f(x)和y=g(x),当且仅当它们的定义域、值域、对应法则都相同时,y=f(x)和y=g(x)才表示同一函数 若两个函数表示同一函数,则它们的图象完全相同,反之亦然
若两个函数表示同一函数,则它们的图象完全相同,反之亦然
解:(1)由于f(x)= =|x|,g(x)=
=|x|,g(x)= =x,故它们的值域及对应法则都不相同,所以它们不是同一函数
=x,故它们的值域及对应法则都不相同,所以它们不是同一函数
(2)由于函数f(x)= 的定义域为(-∞,0)∪(0,+∞),而g(x)=
的定义域为(-∞,0)∪(0,+∞),而g(x)= 的定义域为R,所以它们不是同一函数
的定义域为R,所以它们不是同一函数
(3)由于当n∈N*时,2n±1为奇数,∴f(x)= =x,g(x)=(
=x,g(x)=( )2n-1=x,它们的定义域、值域及对应法则都相同,所以它们是同一函数
)2n-1=x,它们的定义域、值域及对应法则都相同,所以它们是同一函数
(4)由于函数f(x)=
 的定义域为{x|x≥0},而g(x)=
的定义域为{x|x≥0},而g(x)= 的定义域为{x|x≤-1或x≥0},它们的定义域不同,所以它们不是同一函数
的定义域为{x|x≤-1或x≥0},它们的定义域不同,所以它们不是同一函数
(5)函数的定义域、值域和对应法则都相同,所以它们是同一函数
评述:(1)第(5)小题易错判断成它们是不同的函数,原因是对函数的概念理解不透 要知道,在函数的定义域及对应法则f不变的条件下,自变量变换字母,以至变换成其他字母的表达式,这对于函数本身并无影响,比如f(x)=x2+1,f(t)=t2+1,f(u+1)=(u+1)2+1都可视为同一函数
要知道,在函数的定义域及对应法则f不变的条件下,自变量变换字母,以至变换成其他字母的表达式,这对于函数本身并无影响,比如f(x)=x2+1,f(t)=t2+1,f(u+1)=(u+1)2+1都可视为同一函数
(2)对于两个函数来讲,只要函数的三要素中有一要素不相同,则这两个函数就不可能是同一函数
例5 某种细胞分裂时,由1个分裂成2个,2个分裂成4个,…,一直分裂下去.
(1) 用列表表示,1个细胞分裂1、2、3、4、5、6、7、8次后,得到的细胞个数;
(2)用图像表示1个细胞分裂的次数n(nÎN+)与得到的细胞个数y之间的关系;
解:(1) 利用正整指数幂的运算法则,可以算出1个细胞分裂1、2、3、4、5、6、7、8次后,得到的细胞个数,列表如下
|
分裂次数 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
细胞个数 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
(2)细胞个数y与分裂次数n之间的关系式是
y=2n,nÎN+.
变式:
一种专门占据内存的计算机病毒,开机时占据内存 KB,然后每
KB,然后每 分钟自身复制一次,复制后所占内存是原来的
分钟自身复制一次,复制后所占内存是原来的 倍,那么开机后经过 ______ 分钟,该病毒占据
倍,那么开机后经过 ______ 分钟,该病毒占据 MB内存(
MB内存( MB=
MB= KB)
KB)
 例6试构造一个函数
例6试构造一个函数 ,使得对一切
,使得对一切 有
有 恒成立,但是
恒成立,但是 既不是奇函数又不是偶函数,则
既不是奇函数又不是偶函数,则 可以是
可以是

解: 的图像部分关于原点对称,部分关于
的图像部分关于原点对称,部分关于 轴对称,如
轴对称,如
 .
.
点评 本题是一道开放题,你能给出其它的答案吗?请不妨一试.
例7 某厂生产一种仪器,由于受生产能力和技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率 与日产量
与日产量 (件)之间大体满足关系:
(件)之间大体满足关系:
 (其中c为小于96的正常数)
(其中c为小于96的正常数)
注:次品率 ,如
,如 表示每生产10件产品,约有1件为次品.其余为合格品.
表示每生产10件产品,约有1件为次品.其余为合格品.
已知每生产一件合格的仪器可以盈利A元,但每生产一件次品将亏损 元,故厂方希望定出合适的日产量.
元,故厂方希望定出合适的日产量.
(1)试将生产这种仪器每天的盈利额 (元)表示为日产量
(元)表示为日产量 (件)的函数;
(件)的函数;
(2)当日产量为多少时,可获得最大利润?
解:(1)当 时,
时, ,所以,每天的盈利额
,所以,每天的盈利额 ;
;
当 时,
时, ,
,
所以,每日生产的合格仪器约有 件,次品约有
件,次品约有 件.故,每天的盈利额
件.故,每天的盈利额


综上,日盈利额 (元)与日产量
(元)与日产量 (件)的函数关系为:
(件)的函数关系为:

(2)由(1)知,当 时,每天的盈利额为0.
时,每天的盈利额为0.
当 时,
时, .
.
令 ,则
,则 .
.
故 
 .
.
当且仅当 ,即
,即 时,等号成立.
时,等号成立.
所以(i)当 时,
时, (等号当且仅当
(等号当且仅当 时成立).
时成立).
(ii) 当 时,由
时,由 得
得 ,
,
易证函数 在
在 上单调递增(证明过程略).
上单调递增(证明过程略).
所以, .
.
所以,

 ,
,
即 .(等号当且仅当
.(等号当且仅当 时取得)
时取得)
综上,若 ,则当日产量为88件时,可获得最大利润;若
,则当日产量为88件时,可获得最大利润;若 ,则当日产量为
,则当日产量为 时,可获得最大利润.
点评 分段函数是历年高考的热门话题,常考常新,值得我们在复课时认真对待.
时,可获得最大利润.
点评 分段函数是历年高考的热门话题,常考常新,值得我们在复课时认真对待.
例8 矩形 的长
的长 ,宽
,宽 ,动点
,动点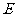 、
、 分别在
分别在 、
、 上,且
上,且 ,(1)将
,(1)将 的面积
的面积 表示为
表示为 的函数
的函数 ,求函数
,求函数 的解析式;
的解析式;
(2)求 的最大值.
的最大值.
解:(1)

 .
.
∵ ,∴
,∴ ,
,
∴函数 的解析式:
的解析式: ;
;
(2)∵ 在
在 上单调递增,
上单调递增,
∴ ,即
,即 的最大值为
的最大值为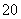 .
.
例9
函数 对一切实数
对一切实数 ,
, 均有
均有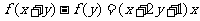 成立,且
成立,且 ,
,
(1)求 的值;
的值;
(2)对任意的 ,
, ,都有
,都有 成立时,求
成立时,求 的取值范围.
的取值范围.
解:(1)由已知等式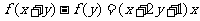 ,
,
令 ,
, 得
得 ,
,
又∵ ,∴
,∴ .
.
(2)由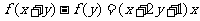 ,
,
令 得
得 ,
,
由(1)知 ,∴
,∴ .
.
∵ ,
,
∴ 在
在 上单调递增,
上单调递增,
∴ .
.
要使任意 ,
, 都有
都有 成立,
成立,
当 时,
时, ,显然不成立.
,显然不成立.
当 时,
时, ,∴
,∴ ,解得
,解得
∴ 的取值范围是
的取值范围是 .
.
学生练习
题组一:
1 设集合A=R,集合B=正实数集,则从集合A到集合B的映射f只可能是
设集合A=R,集合B=正实数集,则从集合A到集合B的映射f只可能是
A f:x→y=|x| B
f:x→y=|x| B f:x→y=
f:x→y= C
C f:x→y=3-x D
f:x→y=3-x D f:x→y=log2(1+|x|)
f:x→y=log2(1+|x|)
解析:指数函数的定义域是R,值域是(0,+∞),所以f是x→y=3-x
答案:C
2 设M={x|-2≤x≤2},N={y|0≤y≤2},函数f(x)的定义域为M,值域为N,则f(x)的图象可以是
设M={x|-2≤x≤2},N={y|0≤y≤2},函数f(x)的定义域为M,值域为N,则f(x)的图象可以是



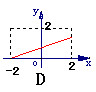
解析:A项定义域为[-2,0],D项值域不是[0,2],C项对任一x都有两个y与之对应,都不符 故选B
故选B 答案:B
答案:B
3 已知函数f(x)=lg
已知函数f(x)=lg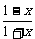 ,若f(a)=b,则f(-a)等于
,若f(a)=b,则f(-a)等于
A b B
b B -b C
-b C
 D
D -
-
解析:f(-a)=lg =-lg
=-lg =-f(a)=-b
=-f(a)=-b 答案: B
答案: B
4 函数y=
函数y= 的定义域是
的定义域是
A [-
[- ,-1)∪(1,
,-1)∪(1, ] B
] B (-
(- ,-1)∪(1,
,-1)∪(1, )
)
C [-2,-1)∪(1,2] D
[-2,-1)∪(1,2] D (-2,-1)∪(1,2)
(-2,-1)∪(1,2)
解析: -
- ≤x<-1或1<x≤
≤x<-1或1<x≤

∴y= 的定义域为[-
的定义域为[- ,-1)∪(1,
,-1)∪(1, ]
] 答案:A
答案:A
5 若函数f(x)=loga(x+1)(a>0,a≠1)的定义域和值域都是[0,1],则a等于
若函数f(x)=loga(x+1)(a>0,a≠1)的定义域和值域都是[0,1],则a等于
A
 B
B
 C
C
 D
D 2
2
解析:f(x)=loga(x+1)的定义域是[0,1],
∴0≤x≤1,则1≤x+1≤2
当a>1时,0=loga1≤loga(x+1)≤loga2=1,∴a=2;
当0<a<1时,loga2≤loga(x+1)≤loga1=0,与值域是[0,1]矛盾
综上,a=2 答案:D
答案:D
6 设集合A和B都是自然数集合N,映射f:A→B把集合A中的元素n映射到集合B中的元素2n+n,则在映射f下,象20的原象是
设集合A和B都是自然数集合N,映射f:A→B把集合A中的元素n映射到集合B中的元素2n+n,则在映射f下,象20的原象是
A 2 B
2 B 3 C
3 C 4 D
4 D 5
5
解析:由2n+n=20求n,用代入法可知选C 答案:C
答案:C
7 某种型号的手机自投放市场以来,经过两次降价,单价由原来的2000元降到1280元,则这种手机平均每次降价的百分率是
某种型号的手机自投放市场以来,经过两次降价,单价由原来的2000元降到1280元,则这种手机平均每次降价的百分率是
A 10% B
10% B 15% C
15% C 18% D
18% D 20%
20%
解析:设降价百分率为x%,
∴2000(1-x%)2=1280 解得x=20
解得x=20 答案:D
答案:D
8 设函数f(x)=
设函数f(x)= 则使得f(x)≥1的自变量x的取值范围为
则使得f(x)≥1的自变量x的取值范围为
A (-∞,-2]∪[0,10] B
(-∞,-2]∪[0,10] B (-∞,-2]∪[0,1]
(-∞,-2]∪[0,1]
C (-∞,-2]∪[1,10] D
(-∞,-2]∪[1,10] D [-2,0]∪[1,10]
[-2,0]∪[1,10]
解析:f(x)是分段函数,故f(x)≥1应分段求解
当x<1时,f(x)≥1 (x+1)2≥1
(x+1)2≥1 x≤-2或x≥0,
x≤-2或x≥0,
∴x≤-2或0≤x<1
当x≥1时,f(x)≥1 4-
4- ≥1
≥1
 ≤3
≤3 x≤10,
x≤10,
∴1≤x≤10
综上所述,x≤-2或0≤x≤10 答案:A
答案:A
9 已知f(x)=
已知f(x)= 则不等式xf(x)+x≤2的解集是________
则不等式xf(x)+x≤2的解集是________
解析:x≥0时,f(x)=1,xf(x)+x≤2 x≤1,∴0≤x≤1;
x≤1,∴0≤x≤1;
当x<0时,f(x)=0,xf(x)+x≤2 x≤2,∴x<0
x≤2,∴x<0 综上x≤1
综上x≤1
答案:{x|x≤1}
10 已知函数y=log
已知函数y=log x与y=kx的图象有公共点A,且A点的横坐标为2,则k的值等于
x与y=kx的图象有公共点A,且A点的横坐标为2,则k的值等于
A -
- B
B
 C
C -
- D
D

解析:由点A在y=log x的图象上可求出A点纵坐标y=log
x的图象上可求出A点纵坐标y=log 2=-
2=-
 又A(2,-
又A(2,- )在y=kx图象上,-
)在y=kx图象上,- =k·2,∴k=-
=k·2,∴k=-
 答案:A
答案:A
11 如图,在边长为4的正方形ABCD上有一点P,沿着折线BCDA由B点(起点)向A点(终点)移动,设P点移动的路程为x,△ABP的面积为y=f(x)
如图,在边长为4的正方形ABCD上有一点P,沿着折线BCDA由B点(起点)向A点(终点)移动,设P点移动的路程为x,△ABP的面积为y=f(x)
(1)求△ABP的面积与P移动的路程间的函数关系式;
 (2)作出函数的图象,并根据图象求y的最大值
(2)作出函数的图象,并根据图象求y的最大值
解:(1)这个函数的定义域为(0,12)
当0<x≤4时,S=f(x)= ·4·x=2x;
·4·x=2x;
当4<x≤8时,S=f(x)=8;
当8<x<12时,S=f(x)= ·4·(12-x)=2(12-x)=24-2x
·4·(12-x)=2(12-x)=24-2x
 ∴这个函数的解析式为
∴这个函数的解析式为
f(x)=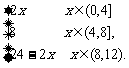
(2)其图形如右, 由图知,[f(x)]max=8
12 若f :y=3x+1是从集合A={1,2,3,k}到集合B={4,7,a4,a2+3a}的一个映射,求自然数a、k的值及集合A、B
若f :y=3x+1是从集合A={1,2,3,k}到集合B={4,7,a4,a2+3a}的一个映射,求自然数a、k的值及集合A、B
解:∵f(1)=3×1+1=4,f(2)=3×2+1=7,f(3)=3×3+1=10,f(k)=3k+1,由映射的定义知
(1) 或(2)
或(2)
∵a∈N,∴方程组(1)无解
解方程组(2),得a=2或a=-5(舍),3k+1=16,3k=15,k=5
∴A={1,2,3,5},B={4,7,10,16}
13 如果函数f(x)=(x+a)3对任意x∈R都有f(1+x)=-f(1-x),试求f(2)+ f(-2)的值
如果函数f(x)=(x+a)3对任意x∈R都有f(1+x)=-f(1-x),试求f(2)+ f(-2)的值
解:∵对任意x∈R,总有f(1+x)=-f(1-x),
∴当x=0时应有f(1+0)=-f(1-0),
即f(1)=-f(1) ∴f(1)=0
∴f(1)=0
又∵f(x)=(x+a)3,∴f(1)=(1+a)3
故有(1+a)3=0 a=-1
a=-1 ∴f(x)=(x-1)3
∴f(x)=(x-1)3
∴f(2)+f(-2)=(2-1)3+(-2-1)3=13+(-3)3=-26
14 集合M={a,b,c},N={-1,0,1},映射f:M→N满足f(a)+f(b)+f(c)=0,那么映射f:M→N的个数是多少?
集合M={a,b,c},N={-1,0,1},映射f:M→N满足f(a)+f(b)+f(c)=0,那么映射f:M→N的个数是多少?
解:∵f(a)∈N,f(b)∈N,f(c)∈N,且f(a)+f(b)+f(c)=0,
∴有0+0+0=0+1+(-1)=0
当f(a)=f(b)=f(c)=0时,只有一个映射;
当f(a)、f(b)、f(c)中恰有一个为0,而另两个分别为1,-1时,有C ·A
·A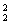 =6个映射
=6个映射 因此所求的映射的个数为1+6=7
因此所求的映射的个数为1+6=7
题组二:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com