
2.解不等式与函数、数列、三角函数、解析几何综合问题的关键是找出各部分的知识点和解法,充分利用相关的知识和方法求解,要依据题设、题断的结构特点、内在联系、选择适当的解决方案,最终归结为不等式的求解、证明或求最值值问题.
1.不等式的性质,解法和证明方法,是综合运用不等式知识解决问题的基础。
4.通过不等式的基本知识、基本方法在代数、三角函数、数列、立体几何、解析几何等各部分知识中的应用,深化数学知识间的融汇贯通,从而提高分析问题解决问题的能力,提高数学素质及创新意识.
3.能从实际问题中抽象出数学模型,找出已知量与未知量,建立数学关系式,并用适当的方法解决问题
2.掌握利用均值不等式和函数单调性求最值的方法,正确理解恒正、恒负、解集为R、解集为空集的实际含义并会等价转换。
1.熟练运用不等式的知识综合解决函数、方程、数列、解析几何等有关问题
11.如下图,四面体ABCD中,E、G分别为BC、AB的中点,F在CD上,H在AD上,且有DF∶FC=2∶3,DH∶HA=2∶3. 求证:EF、GH、BD交于一点.

证明:连结GE、HF,
∵E、G分别为BC、AB的中点,
∴GE∥AC.
又∵DF∶FC=2∶3,DH∶HA=2∶3,
∴HF∥AC.∴GE∥HF.故G、E、F、H四点共面.
又∵EF与GH不能平行,∴EF与GH相交,设交点为O.
则O∈面ABD,O∈面BCD,而平面ABD∩平面BCD=BD.∴EF、GH、BD交于一点.
[探索题]设△ABC和△A1B1C1的三对对应顶点的连线AA1、BB1、CC1相交于一点O,且 =
= =
= =
=  .试求
.试求 的值.
的值.
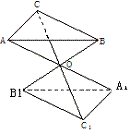
[探索题]解:依题意,因为AA1、BB1、CC1相交于一点O,且 =
= =
= ,所以AB∥A1B1,
,所以AB∥A1B1,
AC∥A1C1,BC∥B1C1.由平移角定理得
∠BAC=∠B1A1C1,∠ABC=∠A1B1C1,△ABC∽△A1B1C1,所以 =(
=( )2=
)2= .
.
10.(2006上海春)在长方体 中,已知
中,已知 ,求异面直线
,求异面直线 与
与 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).

解:连接 ,则
,则 为异面直线
为异面直线 与
与 所成的角.在△
所成的角.在△ 中,
中,

 .
.
 异面直线所成的角为
异面直线所成的角为 .
.
9. 已知正四面体ABCD中,BC的中点为E,AD的中点为F,连AE、CF.(1)判断AE、CF的位置关系;(2)求AE与CF所成的角的余弦.
已知正四面体ABCD中,BC的中点为E,AD的中点为F,连AE、CF.(1)判断AE、CF的位置关系;(2)求AE与CF所成的角的余弦.
答案:
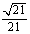
6.异面直线. 7. ; 8.
; 8.  .
.
[解答题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com