
数学综合性试题常常是高考试卷中把关题和压轴题。在高考中举足轻重,高考的区分层次和选拔使命主要靠这类题型来完成预设目标。目前的高考综合题已经由单纯的知识叠加型转化为知识、方法和能力综合型尤其是创新能力型试题。综合题是高考数学试题的精华部分,具有知识容量大、解题方法多、能力要求高、突显数学思想方法的运用以及要求考生具有一定的创新意识和创新能力等特点。
17. 如右图,E、F分别是正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是 .(要求:把可能的图的序号都填上)
如右图,E、F分别是正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是 .(要求:把可能的图的序号都填上)
讲解 因为正方体是对称的几何体,所以四边形BFD1E在该正方体的面上的射影可分为:上下、左右、前后三个方向的射影,也就是在面ABCD、面ABB1A1、面ADD1A1上的射影.
四边形BFD1E在面ABCD和面ABB1A1上的射影相同,如图2所示;
四边形BFD1E在该正方体对角面的ABC1D1内,它在面ADD1A1上的射影显然是一条线段,如图3所示. 故应填23.
18 直线 被抛物线
被抛物线 截得线段的中点坐标是___________.
截得线段的中点坐标是___________.
讲解 由 消去y,化简得
消去y,化简得

设此方程二根为 ,所截线段的中点坐标为
,所截线段的中点坐标为 ,则
,则

故 应填
 .
.
19 椭圆 上的一点P到两焦点的距离的乘积为m,则当m取最大值时,点P的坐标是_____________________.
上的一点P到两焦点的距离的乘积为m,则当m取最大值时,点P的坐标是_____________________.
讲解 记椭圆的二焦点为 ,有
,有

则知

显然当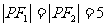 ,即点P位于椭圆的短轴的顶点处时,m取得最大值25.
,即点P位于椭圆的短轴的顶点处时,m取得最大值25.
故应填 或
或
20 一只酒杯的轴截面是抛物线的一部分,它的函数解析式是 ,在杯内放一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的取值范围是___________.
,在杯内放一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的取值范围是___________.
讲解 依抛物线的对称性可知,大圆的圆心在y轴上,并且圆与抛物线切于抛物线的顶点,从而可设大圆的方程为 
由

消去x,得  (*)
(*)
解出  或
或
要使(*)式有且只有一个实数根 ,只要且只需要
,只要且只需要 即
即
再结合半径 ,故应填
,故应填

16. 若四面体各棱的长是1或2,且该四面体不是正四面体,则其体积是 (只需写出一个可能的值).
讲解 本题是一道很好的开放题,解题的开窍点是:每个面的三条棱是怎样构造的,依据“三角形中两边之和大于第三边”,就可否定{1,1,2},从而得出{1,1,1},{1,2,2},{2,2,2}三种形态,再由这三类面构造满足题设条件的四面体,最后计算出这三个四面体的体积分别为:
 ,
, ,
, ,故应填.
,故应填. 、
、 、
、 中的一个即可.
中的一个即可.
15. 过长方体一个顶点的三条棱长为3、4、5, 且它的八个顶点都在同一球面上,这个球的表面积是________.
讲解 长方体的对角线就是外接球的直径 , 即有
, 即有

从而  ,故应填
,故应填
14.
 的展开式中
的展开式中 的系数是
的系数是
讲解 由 知,所求系数应为
知,所求系数应为 的x项的系数与
的x项的系数与 项的系数的和,即有
项的系数的和,即有

故应填1008.
13.某商场开展促销活动,设计一种对奖券,号码从000000到999999. 若号码的奇位数字是不同的奇数,偶位数字均为偶数时,为中奖号码,则中奖面(即中奖号码占全部号码的百分比)为 .
讲解 中奖号码的排列方法是: 奇位数字上排不同的奇数有 种方法,偶位数字上排偶数的方法有
种方法,偶位数字上排偶数的方法有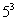 ,从而中奖号码共有
,从而中奖号码共有 种,于是中奖面为
种,于是中奖面为

故应填
12.以下四个命题:
①
②
③凸n边形内角和为 ④凸n边形对角线的条数是
④凸n边形对角线的条数是
其中满足“假设 时命题成立,则当n=k+1时命题也成立’’.但不满足“当
时命题成立,则当n=k+1时命题也成立’’.但不满足“当 (
( 是题中给定的n的初始值)时命题成立”的命题序号是 .
是题中给定的n的初始值)时命题成立”的命题序号是 .
讲解 ①当n=3时, ,不等式成立;
,不等式成立;
② 当n=1时, ,但假设n=k时等式成立,则
,但假设n=k时等式成立,则
 ;
;
③  ,但假设
,但假设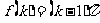 成立,则
成立,则

④  ,假设
,假设 成立,则
成立,则

故应填②③.
11.列 中,
中,
 , 则
, 则

讲解 分类求和,得


 ,故应填
,故应填 .
.
10. 已知 是公差不为零的等差数列,如果
是公差不为零的等差数列,如果 是
是 的前n项和,那么
的前n项和,那么

讲解 特别取 ,有
,有 ,于是有
,于是有
 故应填2.
故应填2.
9.设非零复数 满足
满足  ,则代数式
,则代数式  的值是____________.
的值是____________.
讲解 将已知方程变形为  ,
,
解这个一元二次方程,得

显然有 , 而
, 而 ,于是
,于是
原式=
=
=
在上述解法中,“两边同除”的手法达到了集中变量的目的,这是减少变元的一个上策,值得重视.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com