
7.新航路开辟加速了资本主义的发展,主要是因为()
A、雇佣劳动力增加 B、资本积累速度加快
C、封建制度被消灭 D、资产阶级人数剧增
6.下列哪位航海家率领的船队完成了环球航行()
A、哥伦布 B、麦哲伦 C、迪亚士 D、沃•伽马
5.明清两朝对外实行闭关政策,对此政策的理解正确的是()
A、完全禁绝对外交往 B、禁止商业活动
C、严格限制对外交往 D、禁止官方贸易
4.“凡有麻雀能飞的地方,就有山西商人”,历史上称山西商帮为()
A、晋商 B、湘商 C、粤商 D、徽商
3.“交子”被认为是世界最早使用的纸币,它最早出现在我国的()
A、汉朝 B、唐朝 C、宋朝 D、明朝
2.北京奥运会期间,奥运颁奖礼仪小姐身着“青花瓷”礼服,体现了浓郁的中华传统文化色彩。青花瓷在中国古代哪一时期发展至鼎盛 ( )
A、唐朝 B、宋朝 C、元朝 D、明清
1.“重农抑商”是我国封建社会所推行的一项传统政策。该政策首先实行的时期是(
A、春秋 B、战国 C、唐朝 D、明朝
借助复平面上的两点间的距离公式和直线、圆、圆锥曲线等,再利用复数的意义求解问题,比单纯利用代数计算优越的多。
例12.如果复数z满足︱z+i︱+︱z-i︱=2,那么︱z+i+1︱的最小值是( )
A.1 B.
 C.2 D.
C.2 D.
解析:复平面内满足︱z+i︱+︱z-i︱=2的点z的轨迹是线段AB,而︱z+i+1︱表示点Z到P(-1,-1)的距离如图示,
由图知︱z+i+1︱的最小值是1,选A.
以上十种工具是数形结合中常用的模型,熟练掌握这十种模型及相关知识,可以提高同学们数形结合的能力,。
利用向量可以解决线段相等,直线垂直,立体几何中空间角(异面直线的角、线面角、二面角)和空间距离(点线距、线线距、线面距、面面距),建立坐标系,写出坐标,可以“以数定形”。
例10.如图所示,P是正方形的ABCD的对角线BD上一点,四边形PECF是矩形,
 求证:(1).PA=EF
求证:(1).PA=EF
(2).PA⊥EF
建立如图的坐标系,设正方形的边长是1,︱ ︱=
︱= ,
,
则A(0,1),P(
 ,
,
 ),E(
),E(
 ,0),F(1,
,0),F(1, 
 )
)
∴ =(-
=(-
 ,1-
,1-
 )
) 
 =(
=(
 -1,-
-1,- 
 )
)
(1).∵︱ ︱=(-
︱=(-
 )
) +(1-
+(1-
 )
)
=
 -
-
 +1
+1
︱ ︱=(
︱=(
 -1)
-1) + (-
+ (-
 )
)
=
 -
-
 +1
+1
∴︱ ︱=︱
︱=︱ ︱,即PA=EF
︱,即PA=EF
(2).  ﹡
﹡ =(-
=(-
 )(
)(
 -1)+(1-
-1)+(1-
 )(-
)(-
 )
)
=-

 -
-
 +
+
 +
+

 =0
=0
∴ ⊥
⊥ ,即PA⊥EF
,即PA⊥EF
 例11.如图所示,在棱长为1的正方形ABCD-A
例11.如图所示,在棱长为1的正方形ABCD-A B
B C
C D
D 中,E,F分别是DD
中,E,F分别是DD ,BD的中点,G在棱CD上,且CG=
,BD的中点,G在棱CD上,且CG= CD,H是C
CD,H是C G的中点,
G的中点,
⑴.求证:EF⊥B C
C
⑵.求证:EF与C  G所成角的余弦值
G所成角的余弦值
⑶.求FH的长
解:如图所示,建立空间直角坐标系D-xyz,
E(0,0,  ) F(
) F( ,
, ,0) C(0,1,0) D(0,1,1)
,0) C(0,1,0) D(0,1,1)
B (1,1,1)
G(0,
(1,1,1)
G(0,  ,0)
,0)
(1).证明: =(
=( ,
, ,-
,- )
) 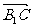 =(-1,0,-1)
=(-1,0,-1)
∵ ·
·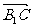 =
= ·(-1)+
·(-1)+  ·0+
·0+ ·(-1)=0
·(-1)=0
∴ ⊥
⊥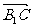 ∴EF⊥B
∴EF⊥B C
C
(2).  =(0,-
=(0,-  ,-1)
,-1)
∴∣ ∣=
∣= =
=
由(1)得
∣ ∣=
∣=
 ·
· =
= ∴cos
∴cos =
=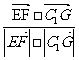 =
=
(3). ∵H是C  G的中点
G的中点
∴H( ,
, ,
, )即H(0,
)即H(0, ,
, )
)
又∵F( ,
, ,0)
,0)
∴FH=︱ ︱=
︱= =
=
点评:利用空间向量解决立体几何问题,将抽象的逻辑论证转化为代数计算,以数助形,大大降低了空间想象能力,是数形结合的深化。
例9.求sin 20
20 +cos
+cos 50
50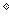 +sin20
+sin20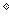 cos50
cos50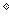 的值。
的值。
解:原式=sin 20
20 +sin
+sin 40
40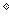 + sin20
+ sin20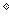 sin40
sin40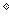
=
sin 20
20 +sin
+sin 40
40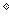 -2 sin20
-2 sin20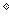 sin40
sin40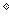 cos120
cos120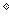
设三角形的外接圆半径是 ,三角形的三边分别是a,b,c,则c= sin20
,三角形的三边分别是a,b,c,则c= sin20 ,b= sin40
,b= sin40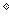
由余弦定理,原式=a =(2·
=(2· ·sin120
·sin120 )
) =
=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com