
5.. (上海市嘉定一中2007学年第一学期高三年级测试(二)) 等差数列{an}共有2n项,其中奇数项的和为90,偶数项的和为72,且 ,则该数列的公差为 ( )
,则该数列的公差为 ( )
A.3 B-3 C.-2 D.-1
答案 B
4.
(2008年天津市十二区县重点学校高三毕业班联考(一))正项等比数列 满足
满足 ,
,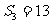 ,
,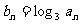 ,则数列
,则数列 的前10项和是
的前10项和是
A.65 B.-65 C.25 D. -25
答案 D
3.(湖南省2008届十二校联考第一次考试)在等比数列 ( )
( )
A. B.
B. C.
C.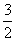 D.
D.
答案 D
2.(山东省潍坊市2007-2008学年度高三第一学期期末考试) 各项都是正数的等比数列 的公比
的公比 ,且
,且 成等差数列,则
成等差数列,则 的值为( )
的值为( )
A. B.
B. C.
C.  D.
D. 或
或
答案 C
1.( 上海市部分重点中学高三第一次联考)
等差数列 的前n项和
的前n项和 当首项
当首项 和公差d变化时,若
和公差d变化时,若 是一个定值,则下列各数中为定值的是―――――――――( )
是一个定值,则下列各数中为定值的是―――――――――( )
A、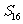 B.
B. S
S C、
C、 D、
D、
答案 B
14.(2009常德期末)已知数列 的前n项和为
的前n项和为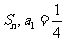 且
且 ,数列
,数列 满足
满足 且
且
 .
.
(1)求 的通项公式;
的通项公式;
(2)求证:数列 为等比数列;
为等比数列;
(3)求 前n项和的最小值.
前n项和的最小值.
解: (1)由 得
得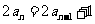 ,
,  ……2分
……2分
∴ ……………………………………4分
……………………………………4分
(2)∵ ,∴
,∴ ,
,
∴ ;
;

∴由上面两式得 ,又
,又
∴数列 是以-30为首项,
是以-30为首项, 为公比的等比数列.…………………8分
为公比的等比数列.…………………8分
(3)由(2)得 ,∴
,∴

=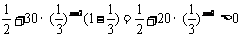 ,∴
,∴ 是递增数列 ………11分
是递增数列 ………11分
当n=1时,  <0;当n=2时,
<0;当n=2时,  <0;当n=3时,
<0;当n=3时,  <0;当n=4时,
<0;当n=4时,  >0,所以,从第4项起的各项均大于0,故前3项之和最小.
>0,所以,从第4项起的各项均大于0,故前3项之和最小.
且 …………………………13分
…………………………13分
2007--2008年联考题
13.(2009龙岩一中)设正整数数列 满足:
满足: ,当
,当 时,有
时,有 .
.
(I) 求 、
、 的值;
的值;
(Ⅱ)求数列 的通项;
的通项;
(Ⅲ)
记 ,证明,对任意
,证明,对任意 ,
, .
.
解(Ⅰ) 时,
时, ,由已知
,由已知 ,得
,得 ,
,
因为 为正整数,所以
为正整数,所以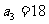 ,同理
,同理 ………………………………2分
………………………………2分
(Ⅱ)由(Ⅰ)可猜想: 。…………………………………………3分
。…………………………………………3分
证明:① 时,命题成立;
时,命题成立;
②假设当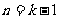 与
与 时成立,即
时成立,即 ,
, 。……………4分
。……………4分
于是 ,整理得:
,整理得: ,……………………………5分
,……………………………5分
由归纳假设得: ,…………………6分
,…………………6分
因为 为正整数,所以
为正整数,所以 ,即当
,即当 时命题仍成立。
时命题仍成立。
综上:由知①②知对于 ,有
,有 成立.………………………………7分
成立.………………………………7分
(Ⅲ)证明:由  ③
③
得  ④
④
③式减④式得  ⑤…………………9分
⑤…………………9分
 ⑥
⑥
⑤式减⑥式得
 …………………11分
…………………11分


 …………13分
…………13分
则  .……………………………………………………14分
.……………………………………………………14分
12.(2009上海九校联考)已知数列 的前
的前 项和为
项和为 ,若
,若 ,则
,则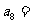 .
.
答案 128
11.(2009南京一模)已知等比数列 的各项均为正数,若
的各项均为正数,若 ,前三项的和为21 ,
,前三项的和为21 ,
则
答案168
10.(2009宁乡一中第三次月考)11、等差数列 中,
中, 且
且 ,则公差
,则公差 =
=
答案 10
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com