
8. 设 是首项为1的正项数列, 且
是首项为1的正项数列, 且
 , 则它的
, 则它的
通项公式是 ____ _____ .
____ _____ .
7. 数列


 前n项和为______ ____.
前n项和为______ ____.
6. 根据市场调查结果, 预测某种家用商品从年初开始的n个月内累积的需求量 (万件)近似
(万件)近似
地满足 . 按此预测, 在本年度内, 需求量超过1.5
. 按此预测, 在本年度内, 需求量超过1.5
万件的月份是 ( )
A. 5月、6月 B. 6月、7月 C. 7月、8月 D. 8月、9月
5. 已知数列 , 那么“对任意的
, 那么“对任意的 , 点
, 点 都在直线
都在直线 上”是“
上”是“
为等差数列”的 ( )
A. 必要而不充分条件 B. 充分而不必要条件
C. 充要条件 D. 既不充分也不必要条件
4. 若数列 前8项的值各异, 且
前8项的值各异, 且 对任意
对任意 都成立, 则下列数列中可取遍
都成立, 则下列数列中可取遍
 前8项值的数列为
( )
前8项值的数列为
( )
A.  B.
B.  C.
C.  D.
D. 
3. 设 , 那么
, 那么 等于 ( )
等于 ( )
A.  B.
B.

C.  D.
D.

2. 设数列 是递增等差数列, 前三项的和为12, 前三项的积为48, 则它的首项是 ( )
是递增等差数列, 前三项的和为12, 前三项的积为48, 则它的首项是 ( )
A. 1 B. 2 C. 4 D. 6
1. 数列 的通项公式为
的通项公式为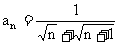 , 若
, 若 前n项和为24, 则n为
( )
前n项和为24, 则n为
( )
A. 25 B. 576 C. 624 D. 625
12. 解: (1) .
.
(2) ∵ , ∴
, ∴
∴ 是首相为
是首相为 , 公差为1的等差数列.
, 公差为1的等差数列.

(3) 在
在 上是增函数.
上是增函数.
证明: 设



∵ , ∴
, ∴ 由当
由当 时,
时, 

即 , ∴
, ∴ 在R上是增函数.
在R上是增函数.
11. 解: 由p得
 , 设
, 设
∴ 在R上的最小值为2c, 即
在R上的最小值为2c, 即 , ∴
, ∴
的解集为R的充要条件是 , 即
, 即
如果p正确, 且q不正确,则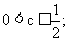 如果p不正确, 且q正确, 则
如果p不正确, 且q正确, 则 .
.
综上所述, c的取值范围为 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com