
1.  ( )
( )
A. 2
B.  C. 4
D.
C. 4
D. 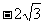
13. 解: (1) 设等比数列 的公比为q, 则
的公比为q, 则 ∴
∴ 或
或 ,
,
∵ 的各项均为正数, ∴
的各项均为正数, ∴ . 所以
. 所以
 .
.
(2) 由
 得
得 . 数列
. 数列 是等差数列,
是等差数列, 
 ,
,
而


∵
∴当 时,
时,  . ∴当
. ∴当 时,
时,  .
.
12. (1)
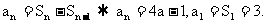

(2) 设抽去是第k项则有:  ,
,
 移项得:
移项得:
 ,
,
所以抽去的是79, 
11. 解: (1) 由
 得
得



由 , 得
, 得
又 ,
所以
,
所以
∴ 数列 的通项公式为
的通项公式为 ;
;
(2)由(1)可知 是首项为
是首项为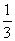 , 公比为
, 公比为 项数为n的等比数列,
项数为n的等比数列,
∴
7.  ; 8.
; 8.  9. 2 , 8 ; 10. 10
.
9. 2 , 8 ; 10. 10
.
(二) 专题测试与练习
(一) 典型例题
例1. 解: 故
故
例2. 解:(1)  ,
, 


所以,

(2)  所以
所以
同理 ……,
……,
所以



由此得 于是
于是

 的通项公式为:
的通项公式为:
当n为奇数时,  当n为偶数时,
当n为偶数时, 
例3. 解:(1)  或
或 .
.
 取
取 .
.
(2) 
假设存在, 则有
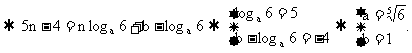
 存在
存在 , 使
, 使 成立.
成立.
11. 数列 的前n项和为
的前n项和为 , 且
, 且 ,
, 
 求
求
(1)  ,
, ,
, 的值及数列
的值及数列 的通项公式; (2)
的通项公式; (2)  的值.
的值.
12. 有穷数列 的前n项和S n=2n2+n, 现从中抽取某一项(不是首项和末项)后, 余下项的
的前n项和S n=2n2+n, 现从中抽取某一项(不是首项和末项)后, 余下项的
平均值是79. (1)求数列 的通项; (2)求数列
的通项; (2)求数列 的项数及抽取的项数.
的项数及抽取的项数.
13. 已知等比数列 共有m项
共有m项 , 且各项均为正数,
, 且各项均为正数,  ,
,  +
+ +
+ .
.
(1) 求数列 的通项
的通项 ;
;
(2) 若数列 是等差数列, 且
是等差数列, 且 ,
,  , 判断数列
, 判断数列 前m项的和
前m项的和 与数列
与数列 的前m项和
的前m项和 的大小并加以证明.
的大小并加以证明.
数列的综合运用解答
10. 在各项均为正数的等比数列 中, 若
中, 若 则
则
 .
.
9. 已知一个等比数列首项为1, 项数是偶数, 其奇数项之和为85, 偶数项之和为170, 求这个
数列的公比 , 项数为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com